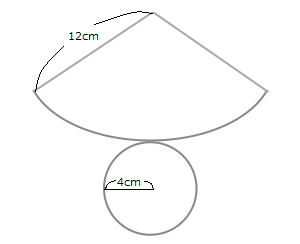
円錐では裏ワザが使えまして 側面のおうぎ形の中心角=母線 分の 底面の半径×360 と言うものです。 これに当てはめていくと答えは12cmになると思います。違っていたらすみません中心角の簡単な求め方教えてください! 上本 き形の中心久の求め方 しpro 半径5cm, 弧の長さご 4z cm のおうぎ形0 申訪角の大きさを求めます。 円とおうぎ形 中心角 簡単な 求め方おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の

扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw
おうぎ形 中心角 裏ワザ
おうぎ形 中心角 裏ワザ- 円錐の表面積は、上の公式を覚えておけば楽勝だよ♪ それでは、例題を使って円錐の表面積の求め方を確認してみましょう。 次の円錐の表面積を求めなさい。 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 次は母線と半径をかけて(Thu) おうぎ形の面積は 半径 × 半径 × π × 中心角/360 という公式を使えば 出すことができましたね。 しかし、下の図のように 肝心の中心角がわかっていない場合 弧の長さを使って中心角を出してから 面積を出さないといけないので



中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ
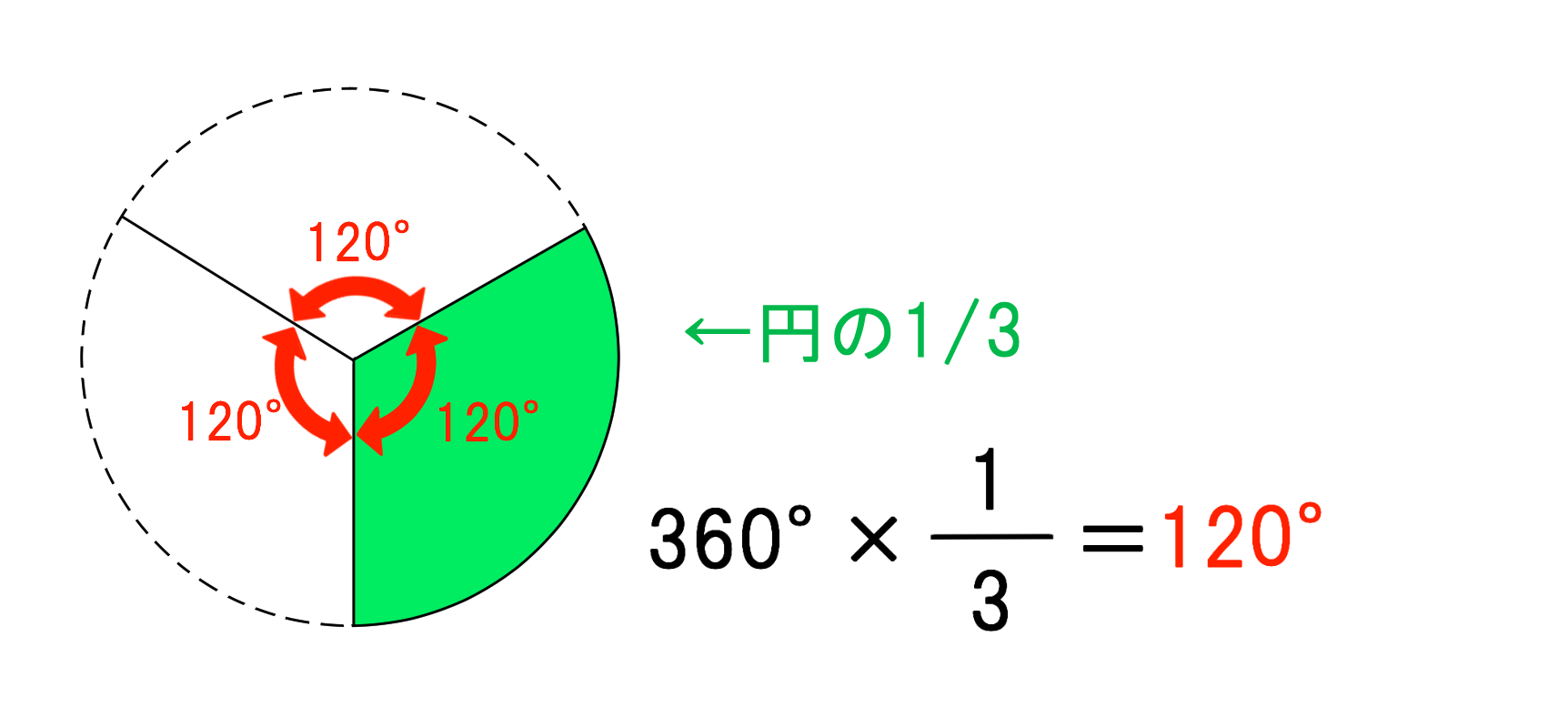
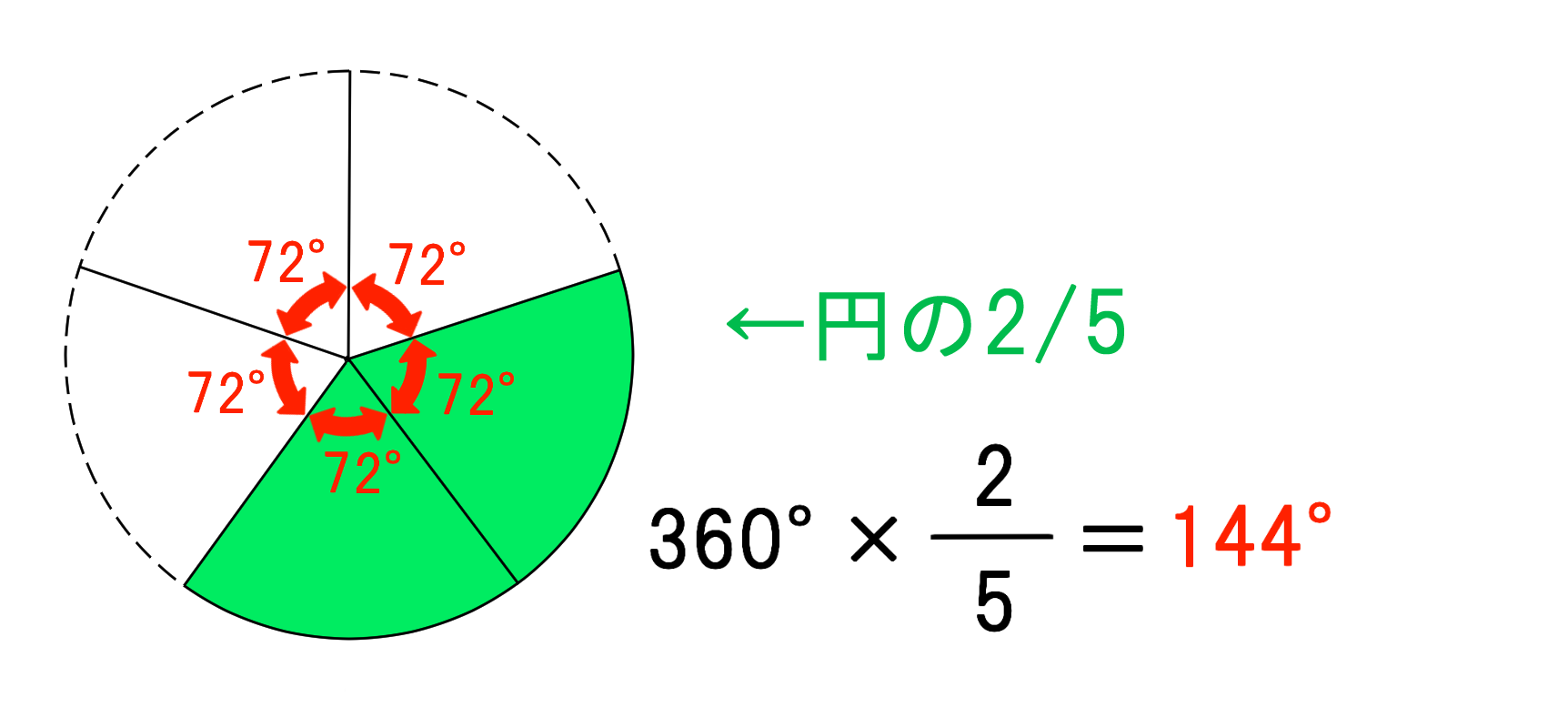
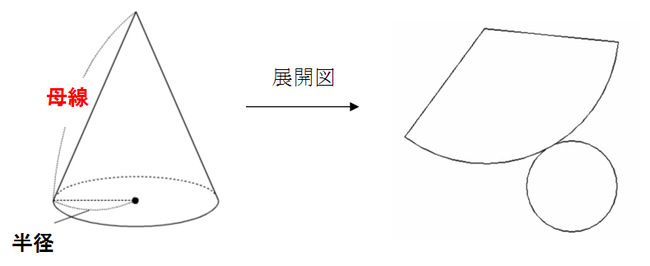
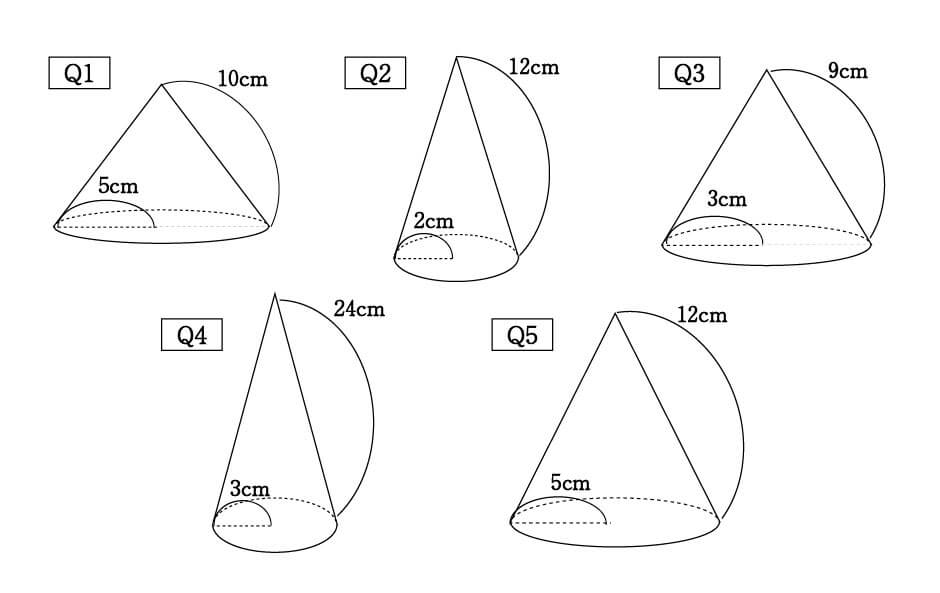
例題:次の円すいの展開したときのおうぎ形の中心角を求めなさい。 (1)$360°× \frac{3}{5}=216°$ (2)$360°× \frac{2}{6}=1°$ 簡単ですね^^ 円すいのおうぎ形中心角のトレーニング! では仕上げのトレーニング! こちらも制限時間は1分です! 今回の中1数学の解説は「おうぎ形の中心角の求め方」についてです。 弧の長さや面積が与えられている時どのようにして中心角を求めるのかを確認していきましょう。 hissoritophysmathcom 今回は ・円錐の中心角の求め方 についてです。 弧の長 半径が3㎝、弧の長さが3 ㎝の扇形の中心角を求めなさい。 まずは、方程式を使って扇形を求める方法について解説していきます。 求めたい中心角を とおいて、方程式を作っていきます。 中心角を とすると、問題文から弧の長さが与えられているので と
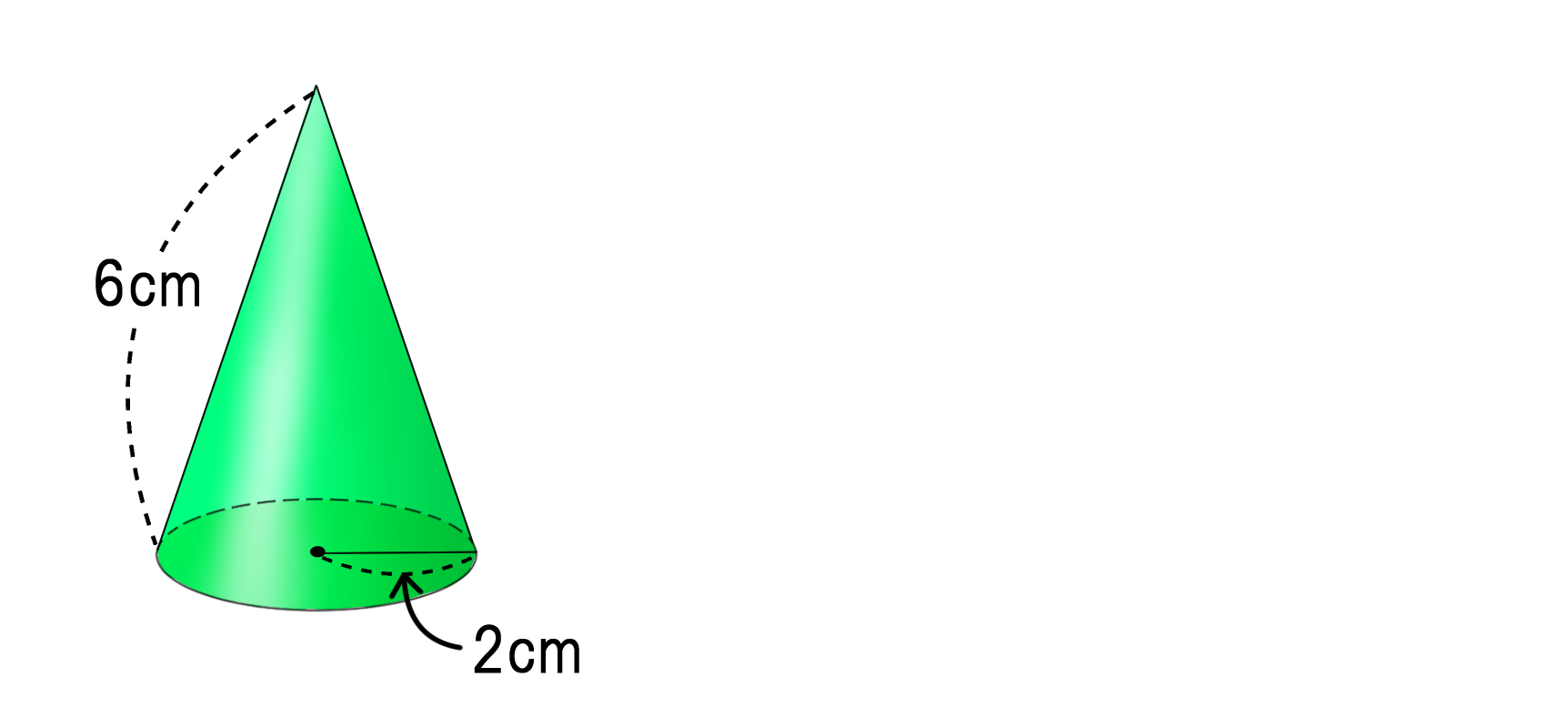
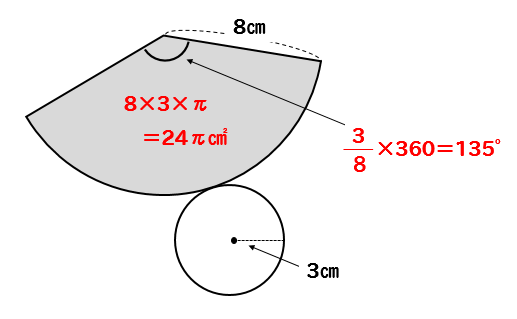
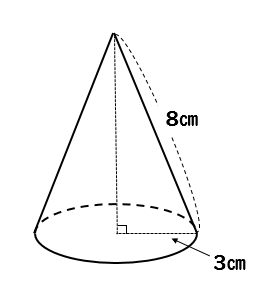
扇形の中心角と弧の長さは比例します。 角度が 「 °」であれば、 弧の長さ=円周×中心角÷360 という式になります。中心角を求める形にするなら 中心角=弧の長さ÷円周×360 円周は半径から出せますから とも表せます。中心角が分からない扇形の面積の求め方の裏ワザ 今回は、勉強のことだよ。 中心角が分からない扇形の面積の求め方の裏ワザだよ。 ↓これ この扇形の弧の長さを15㎝、 AからCの長さは10cmにするよ。 この問題を普通にやると、側面のおうぎ形の 弧の長さ は、 底面の円周と同じ長さ になります。 半径 $3 \rm cm$ の円なので、$2×3×π=\textcolor{red}{6π\rm cm}$ 問題側面のおうぎ形の中心角の大きさを求めなさい。 側面のおうぎ形は半径 $5 \rm cm$ の 円の一部 といえます。
例題 《円錐側面の中心角》 演習try 下の図の円錐の展開図をかくとき,側面になるおう ぎ形の中心角を求めなさい。 裏ワザ公式を覚えておけば楽勝! 下の図の円錐の展開図をかくとき,側面になるおうぎ形 の中心角を求めなさい。 1つめは展開図を書いた時のおうぎ形の中心角の求める問題 もうひとつは、展開図を書いた時のおうぎ形の部分(側面席)を求める問題 これらについて、「秒殺で解ける裏ワザ」の確認! あと、円錐を転がす問題。これもよう出る!数学 中学 数学すべての科目学習内容 平面図形 おうぎ形の中心角の求め方 「うちの子、大丈夫かな? 」 と1人で悩んでいませんか? 学習習慣が身につかず、成績が伸びない 反抗期でどう接したらいいかわからない 友達関係に悩んでいそう




3学期学年末テストの攻略 中1数学 Klcブログ



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学
例題 《円錐側面の中心角》 演習try 下の図の円錐の展開図をかくとき,側面になるおう ぎ形の中心角を求めなさい。 裏ワザ公式を覚えておけば楽勝! 下の図の円錐の展開図をかくとき,側面になるおうぎ形 の中心角を求めなさい。 ⑤ も × ※ = 6 × 3 6 ⑤おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 1.おうぎ形を円の一部分と考えると、この円は半径が12cmですよ ね。 ということは、この円の円周の長さは2×12×π 2.おうぎ形の弧は円の一部ですね。 円の中心角は360度ですから、 その一部である10π となる中心角は比例式で得られますね。 0 件 通報



三角形のノリでおうぎ形を攻略する 種池校 成績保証の個別指導学習塾wam



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学
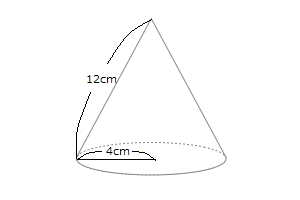
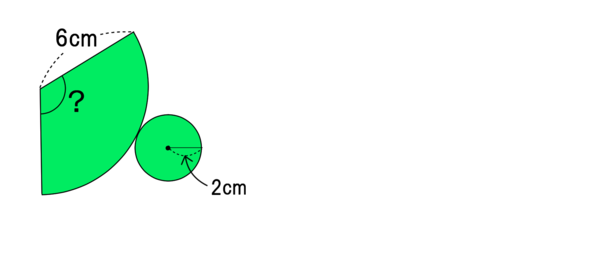
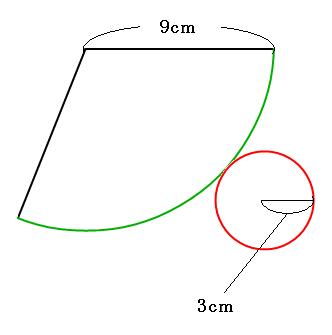
おうぎ形の中心角 a=360×(r/R) イイネ! コメント 11 mixiユーザー 02月25日 1353 三角形の面積 (ab)/2 放物線でおなじみですよね。 イイネ! コメント 12 mixiユーザー 02月25日 1356 台形を対角線で三角形4つに分けたときのそれぞれの面積比楽しい数学:『中心角の裏ワザ』 『 底面の半径3cm、母線の長さ5cmの円すいの側面のおうぎ形の中心角を求めなさい。 』 この問題も円すいを展開図にしてから考えます。 展開図にすると、オレンジの部分が側面、白い円が底面になります。 つまり おうぎ形の弧の長さを求める方法 \(2\pi r\times\frac{a}{360}\) を利用すれば、式自体はすぐに立てられる。しかし分数などあり、方程式を解くのが少々面倒に感じる人も多いだろう。 そこで、比を利用する。円は、中心角が360°であることを利用すればいい。



Math 円の問題を解くときに使う3つの技 全体 白 分配法則 移動 働きアリ




中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ
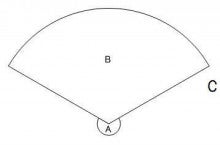
「扇形の中心角」が360°中どれだけ大きいか?? ということをみればいい。だって、円の中心角はぐるっと回った360°だからね。 だから、おうぎ形パワーは中心角αを360°でわった、 α/360 になるんだ。 これはなんという偶然か、ピザを切り分けるときと一緒。 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね 中心角が \(180^\circ\) なので、底面の上に半径 \(6 \ \mathrm{cm}\) の半円を書きます。 底面とおうぎ形が \(1\) 点で交わるように、底面とおうぎ形の接点から書き始めるときれいに書けま




扇形の中心角の人気動画を探索しましょう Tiktok




楽しい数学 中心角の裏ワザ 塾のおしごと
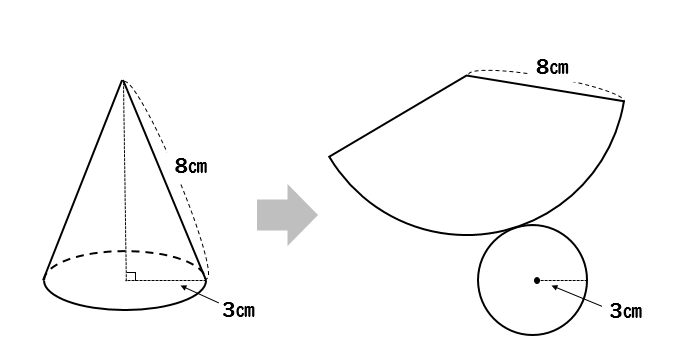
側面の中心角の求め方について解説していきます。 まず、円錐の展開図は このように、おうぎ形と円が組み合わさった形になります。 そして、ポイントとなるのが 側面であるおうぎ形の弧の長さと 底面である円の円周の長さが等しくなります 扇形の中心角の求め方3パターン を見てみてね ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線 こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど! 何を求めるのも公式だより おうぎ形の中心角を求める おうぎ形の弧の長さ は、 円の円周 と同じ長さなので $14cm$ また、このおうぎ形の元となった円(半径$5cm$)の円周の長さは、 $5\times2\times314=314cm$ おうぎ形の弧の長さと、元の円周(半径$5cm$)の長さを比べると




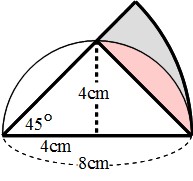
この問題の求め方がわかりません 中心角45度の扇形からどこをひけばよいのでし Clearnote




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
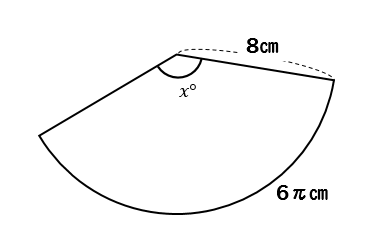
おうぎ形の問題では弧の長さや面積を求める問題が出題されますが、それぞれ以下の公式で求めることができます。 おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と 弧 の 長 さ 半 径 中 心 角 弧 の 長 さ = 半 径 × 2 × 314 × 中 心 角 360 ∘ 中心角のわかっている、おうぎ型の 面積 を求める公式 面 積 半 径 半 径 中 心 角 面 積 = 半 径 × 半 径 × 314 × 中 心 角 360 ∘ 面積を2倍 にすると 面 積 半 径 半 径 中 心 角 面 積 × 左辺を「中心角の比」、右辺を「弧の長さの比」で比例式をたててみよう。すると、 (扇形の中心角):(円の中心角) = (扇形の弧の長さ):(円周の長さ) x 360 = 6π 8π ってなるよー。 Step3 比例式を「内項・外項の積」でとく!



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
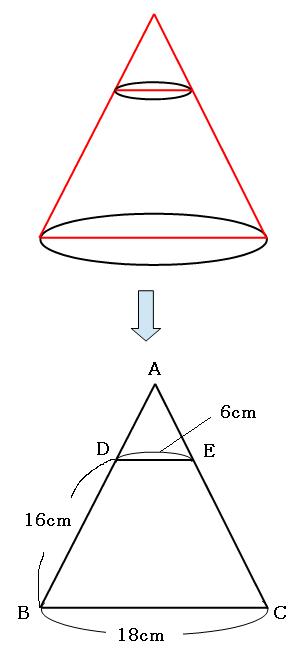



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
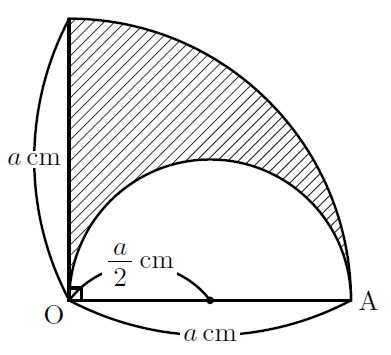
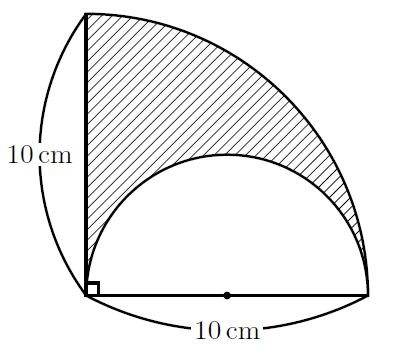
おうぎ形の弧の長さ、面積、中心角の求め方と公式 19 February 16 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は 1 8 0 ∘ 180^\circ 180∘ 、さらに半分切りとれば中心角は 9 0 ∘ 90^\circ 90∘ になります。 ケーキを半分に切ったり、三分 半径 cm,中心角90 の扇形と半径 cmで中心角180 の扇形が図のように線分OAでぴったり重なっていることを考える。このとき斜線部分の面積は次のように与えられる。 の扇形・半径 半円・半径 ここで半径 cm,中心角180 の扇形の面積は,



三角形のノリでおうぎ形を攻略する 種池校 成績保証の個別指導学習塾wam




表面積の問題で 中心角の求め方が分からず答えを見たんですが 説明文の意味がわ Clearnote




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




楽しい数学 中心角の裏ワザ 塾のおしごと




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw
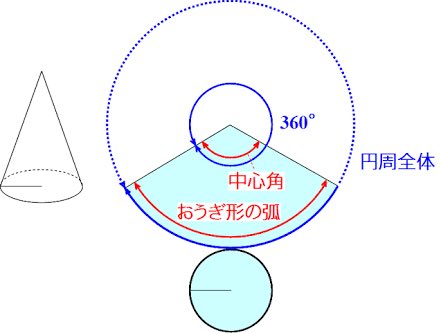



高校受験対策laf先生 円錐の側面 扇形 の中心角を簡単に求める公式 裏技 中心角 360 底面の半径 母線 中心角を求めるのは手間がかかりますが こちらの裏技で簡単に求めることができます 理由は写真でチェック



中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ



おうぎ形の裏技 面積公式 個太郎塾



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典



おうぎ形の中心角の求め方を教えてください 半径5cm Yahoo 知恵袋




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




この問題の求め方がわかりません 中心角45度の扇形からどこをひけばよいのでし Clearnote



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




あきとんとん数学空間図形 Mp3



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学



中心角が分からない扇形の面積の求め方の裏ワザ 爽のつぼやき




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




Kpmix28pr2clpm



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学




4 1 2 ともにわかりません Clearnote




裏ワザ 円錐の表面積とおうぎ形の中心角 超簡単 Youtube




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




難しい問題の解き方 の解説 円とおうぎ形の周りの長さ 面積を求める応用問題3選 中学受験ナビ



3




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



3月8日更新 授業日記 おうぎ形の中心角 成績 上がってます 根城学習塾 八戸市




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




図形の裏ワザ 知っていたら数秒で解ける あまり知られていない裏ワザ 2問 Youtube



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw



円すいの表面積 おうぎ形の中心角 簡単に求まります Net家庭学習支援塾




数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




おうぎ形 Twitter Search Twitter




楽しい数学 中心角の裏ワザ 塾のおしごと




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



Mathematics 平面図形 おうぎ形 働きアリ



1
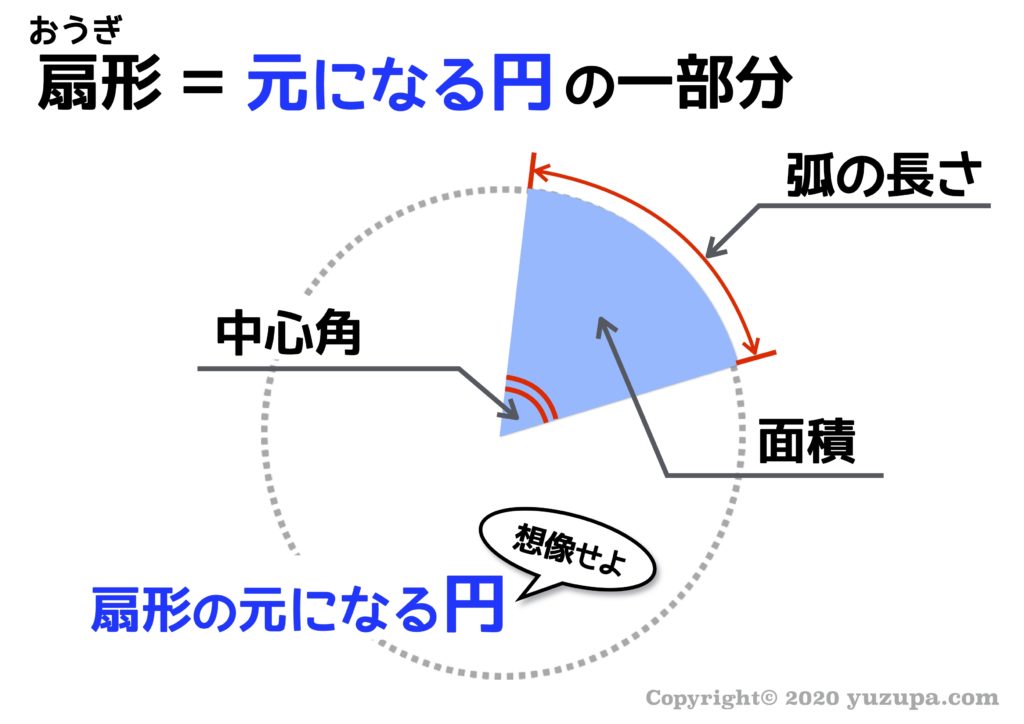



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋
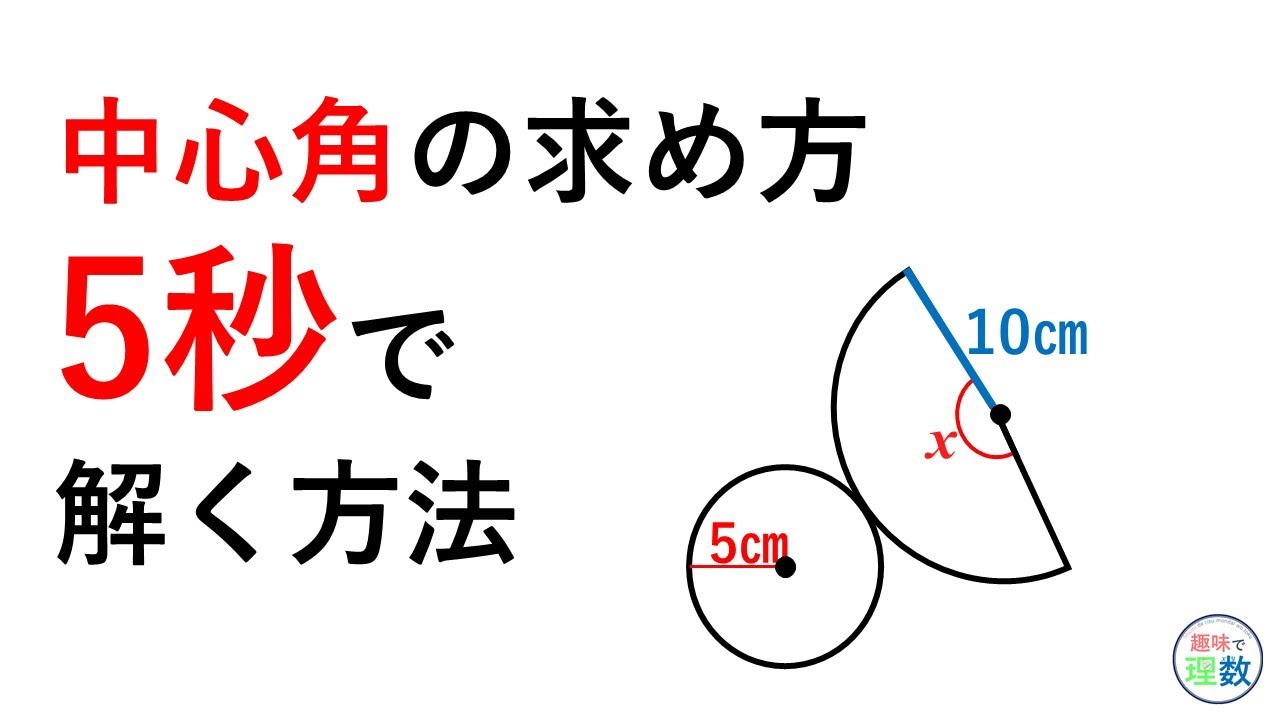



おうぎ形の中心角の求め方 Youtube



おうぎ形の中心角の求め方の裏技みたいなのありますか Yahoo 知恵袋




楽しい数学 中心角の裏ワザ 塾のおしごと




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




中心角の人気動画を探索しましょう Tiktok




おうぎ形 中心角の求め方の人気動画を探索しましょう Tiktok




中学数学 知って役立つ 裏ワザ 公式 家庭教師のノーバス




中学数学 扇形の面積と弧の公式 中心角がなくても求まる 中1数学 Youtube




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという Clearnote




3学期学年末テストの攻略 中1数学 Klcブログ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形裏ワザの人気動画を探索しましょう Tiktok




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ



円錐の表面積の求め方



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋



1




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル
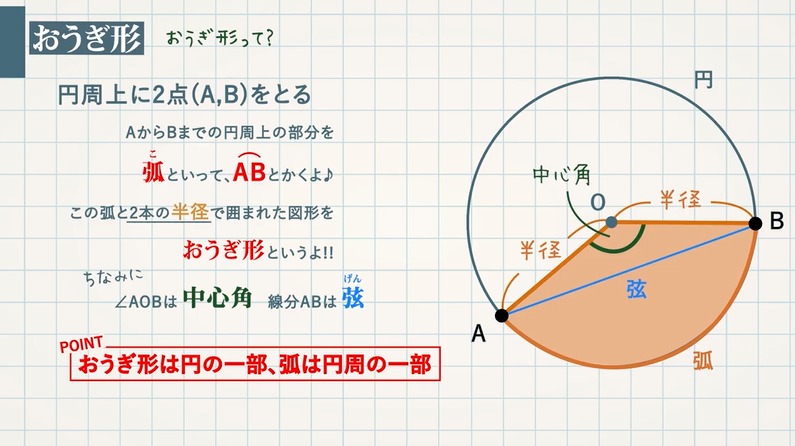



おうぎ形まとめ 弧と面積の求め方 教遊者




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



半径4cm面積6pcm の扇形の中心角の求め方を教えてください Yahoo 知恵袋




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




楽しい数学 中心角の裏ワザ 塾のおしごと




数学裏ワザ 2 円すいの側面を展開してできるおうぎ形の中心角を一瞬で出す方法を紹介 テストで使える Youtube
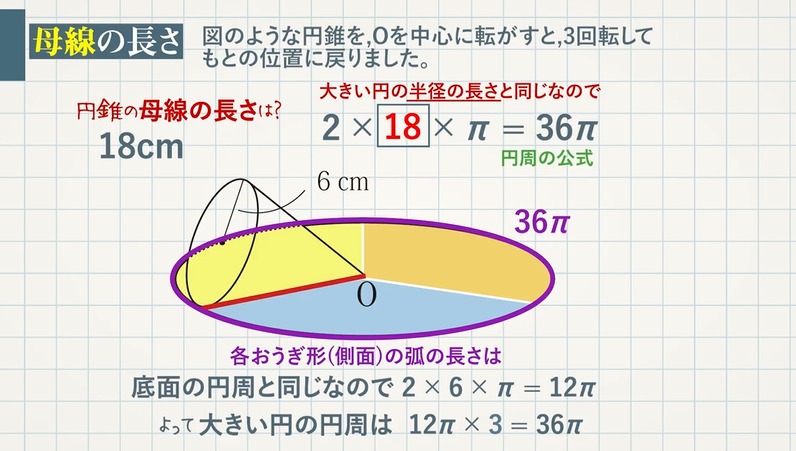



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



おうぎ形の中心角の求め方の裏技みたいなのありますか Yahoo 知恵袋




数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




3学期学年末テストの攻略 中1数学 Klcブログ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




この問題の求め方がわかりません 中心角45度の扇形からどこをひけばよいのでし Clearnote




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




解き方を分かりやすく教えて欲しいです 未だにおうぎ形の公式が曖昧でま Clearnote



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中1のおうぎ形の中心角の求め方の公式を教えてください Yahoo 知恵袋




楽しい数学 中心角の裏ワザ 塾のおしごと



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
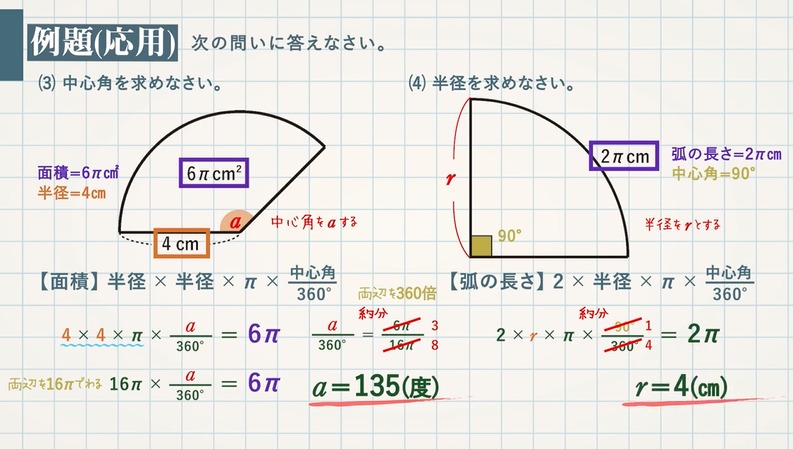



おうぎ形まとめ 弧と面積の求め方 教遊者



0 件のコメント:
コメントを投稿