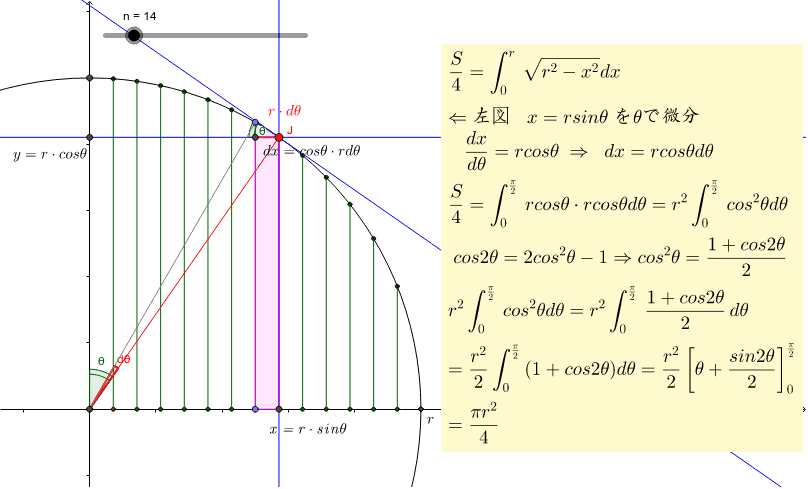
他の面積公式との関係 この面積公式をもとに他の面積公式を導出することができます。 例えば,この公式と正弦定理を用いることで対称な式: S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます( R R R は三角形 A B C ABC A BC の外接円の半径)。 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式 まずは公式を書いておきます。 半径を \(r\) として \(V=\displaystyle\frac{4}{3}\pi r^3\) 証明円の面積の公式の証明 いよいよ円の面積の公式を証明する準備が整った ようである。 原点中心、半径 r の円の方程式は、 X 2 +Y 2 =r 2 により与えられる。その四分円の面積を S とおくと、

円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト
円 面積 公式 角度
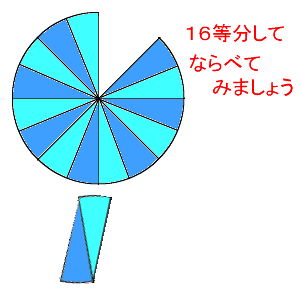
円 面積 公式 角度-円の面積の公式をつくってみよう。 《3/5の展開》 3 / 5 ・ 円を16等分したおうぎ形を並べ、その形から面積を推測する。 ・ 既習の図形と関連付けて円の面積の公式を考える。 (作業的な活動) (説長方形の縦の長さは,円の半径,横の長さは,円周の半分と同じになります。 積の公式は次のようになります。 円の面積=半径×円周の半分 円周 半分 直径 =半径×半径×314 円の面積 チャレンジシート① 学ぶ 円の面積=半径×半径×314 円周の半分(半径×3



円の面積計算 ゆるゆるプログラミング
円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h面積計算機 円 公式 円周長から面積台形の面積 台形の高さ・面積 (4辺の長さから) 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積
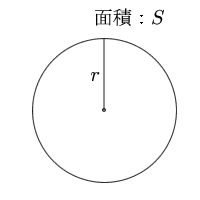
円周の長さ = 直径 × 円周率楕円の面積公式 \dfrac {x^2} {a^2}\dfrac {y^2} {b^2}=1 \ (a, b > 0) a2x2 b2y2 = 1(a,b > 0) で表される楕円の面積円の面積の求め方を考 え、説明できる。 分割してできた扇形を並べ替え ると、平行四辺形から長方形に近 づいていくことを確かめる。 円を変形させた長方形の面積を 求める。 円の面積を求める公式をまとめ る。 ② ① ノート 発表や発言
円の面積=半径×半径×3.14 教え方4 教え方 4 練習問題を通して、円の面積の勉強のおさらいをさせます。 最後に この勉強では、円の面積を求める公式を使って、円の面積やいろいろな形の面積を求めることをねらいとしています。 中学校では次のような公式を習うかと思います。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r円の断面積と公式 円の断面積の公式は、下記です。 A=πr 2 Aは円の断面積、πは円周率(概ね314)、rは円の半径です。上記の公式は、「ぱいあーるじじょう」と読んで、覚えましょう(覚えやすいと思います)。 また、直径を用いた公式もあります。




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの円の面積a=πd 2 /4です。 また半径rを使えばA=πr 2 で算定できます。 直径と半径の関係、円の面積の詳細など下記も参考になります。




円の面積計算 ゆるゆるプログラミング



円の面積の公式 算数の公式
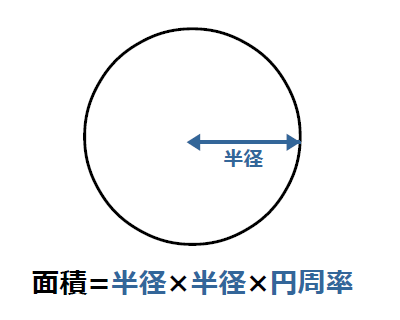
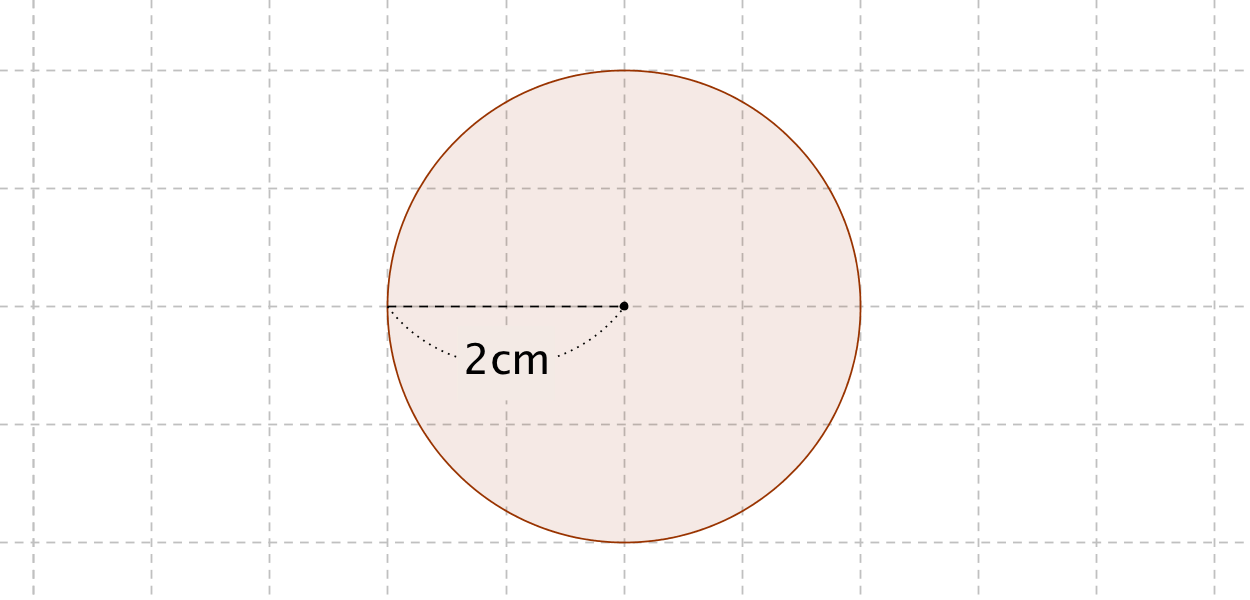
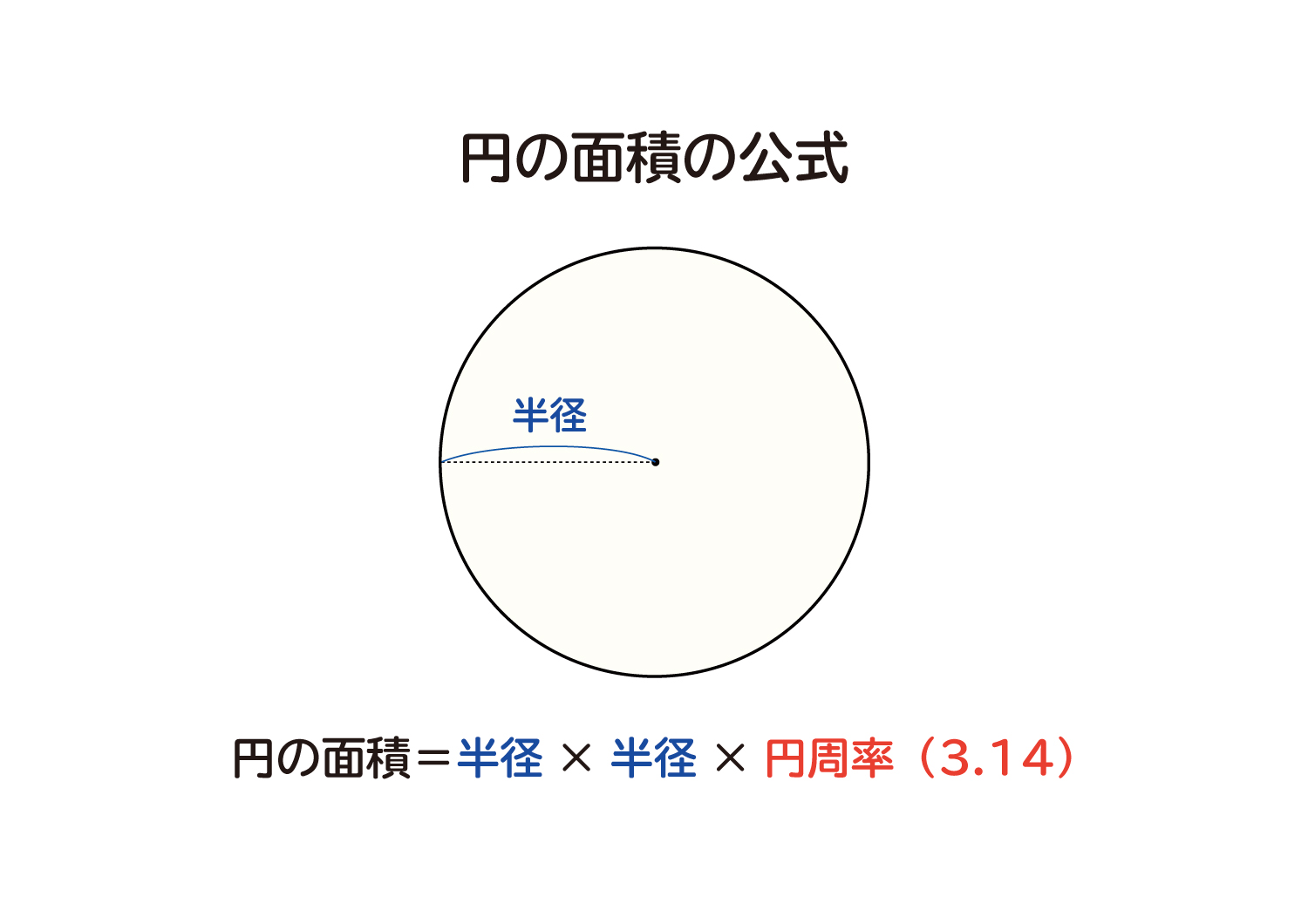
円の面積の公式をつくってみよう。 《3/5の展開》 3 / 5 ・ 円を16等分したおうぎ形を並べ、その形から面積を推測する。 ・ 既習の図形と関連付けて、円の面積の公式を考える。 (作業的な活動) (説明する活動)円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 答え: 2 × 2 × 314 = 1256 (cm 2) 正確には 2 × 2 × π = 4 π




円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo



小6算数 円の面積 指導アイデア 1 みんなの教育技術
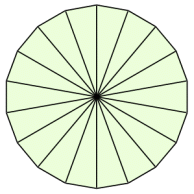
円の面積が「半径×半径×円周率(314)」になる説明 円の面積の公式を下のような図を使って確認してみたいと思います。 この円を、細かく等分に分けます。そして、等分に分けた上と下を並べると、長方形に近い形になります。 この円を、先ほどよりもっと細かく分けてみると、さっきより ドーナツ状の図形の面積を求めたい。 直径センチ 中の円は3センチ この条件しか分かりません。 直径だけで出せる公式ありますか? 純粋に大きい円の面積ー中の円=ドーナツの面積って話なら分かります。(1)円や球の求積公式の導出法 ① 円の面積公式の導出法 半径r の円の面積S は,例えば,次のようにして求 めることができる。 関数 x のグラフと 軸で囲ま れる部分の面積は半円の面積を表すので, で




円の面積 算数用語集




円柱の表面積と体積を求める公式 具体例で学ぶ数学
まず、円の面積と円周は以下の公式で求められます。 円の面積 S =πr2 S = π r 2 円周 l=2πr l = 2 π r円の面積を公式を使っ て求めることができる。 ・円の面積を求める公式を考える。 ・円の面積を求める公式をまとめる。 思表判円の分割・合成 の操作から、円の面 積の求め方を筋道立 てて考え、公式を導 き出している。 知技円の面積を、公式三角形の面積は『底辺×高さ ÷2 ÷ 2 』です。 ここでは 「底辺:元の円の円周(直径×円周率)」 、 「高さ:元の円の半径」 にあたります。 また、直径を 2 2 で割ると半径になります。
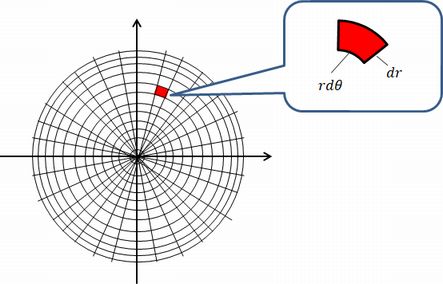



極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau
A=面積 A=ab a=A÷b b=A÷a (備考)a寸法はb辺に対し 直角に測ったもの A=面積 A=π(R 2r 2)=π(Rr)(Rr) =(D 2d 2) =(Dd)(Dd) A=面積 A=面積 A=面積 もし とすれば A=面積 A=面積 もし とすれば A=面積 P=楕円の周囲 A=πab 、Pを求める近似式 A=面積 A=面積BCD A=面積 円の面積・・・半径×半径×π=πr² 円周・・・直径×π=2πr ここで登場するのが、『微分』です。 r²を微分すると2rになります。 つまり、円の面積を微分すると円周の公式になります。 球の体積・・・4πr³/3 球の表面積・・・4πr²8 rader 円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
A=面積 楕 円 双 曲 線 放 物 線 (すなわちχを底辺としYを高さとする短形の面積の2/3に等しい) 放物線切片 サイクロイド①円の半径と面積の関係の理解 ②円の面積の公式の理解 ③公式を使って、円の面積を求めること ④円や三角形をもとにして、曲線の図形の面積を求めること 教え方1 円の面積の大きさを順々に予想させていきます。 教え方1円の面積 「半径×半径×円周率」で求められる円の面積。 いろいろな大きさの円の面積を計算してみよう。 動画で学ぼう! (NHK for School) 円の面積の求め方を、四角に直すことで原理から考える




三角形の面積を外接円の半径を使って求める Schoolmath S Diary



盲点の英単語 その8 円の面積の求め方を英語で言える 中学の英語をあなどってはいけない
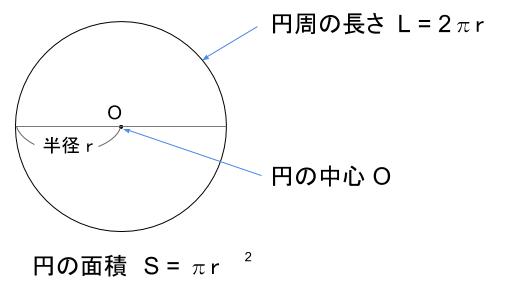
② 半径5cmの円の面積 式 5×5×314 8 人(30%) 答え 785㎠ 8 人(30%)ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




無差別級算数 円の面積 2 解答 受験算数に挑戦
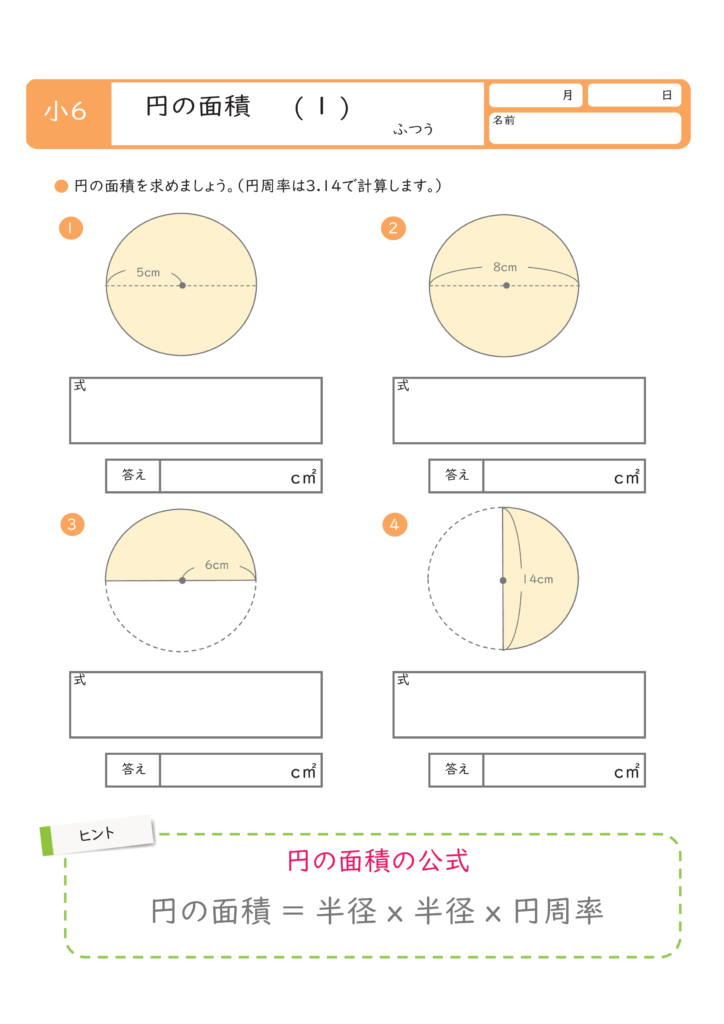
半径 $r$ の円の面積 $S$ は、次の公式で求められます。 円 (えん) の面積 \begin{align*} S = \pi r^2 \end{align*} 面積 = 半径 × 半径 × 314 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「円の面積の求め方」をご覧ください。
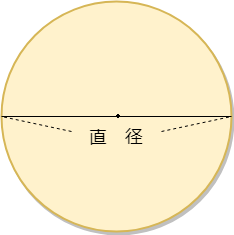



円の面積 円周の求め方 公式 小学生 中学生の勉強




山と数学 そして英語 小学校算数 円の面積に関する応用問題




円の面積の公式 算数の公式




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張
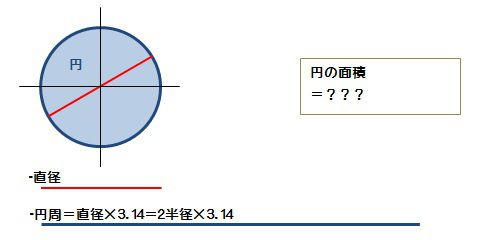



円の面積 算数の公式覚えてますか
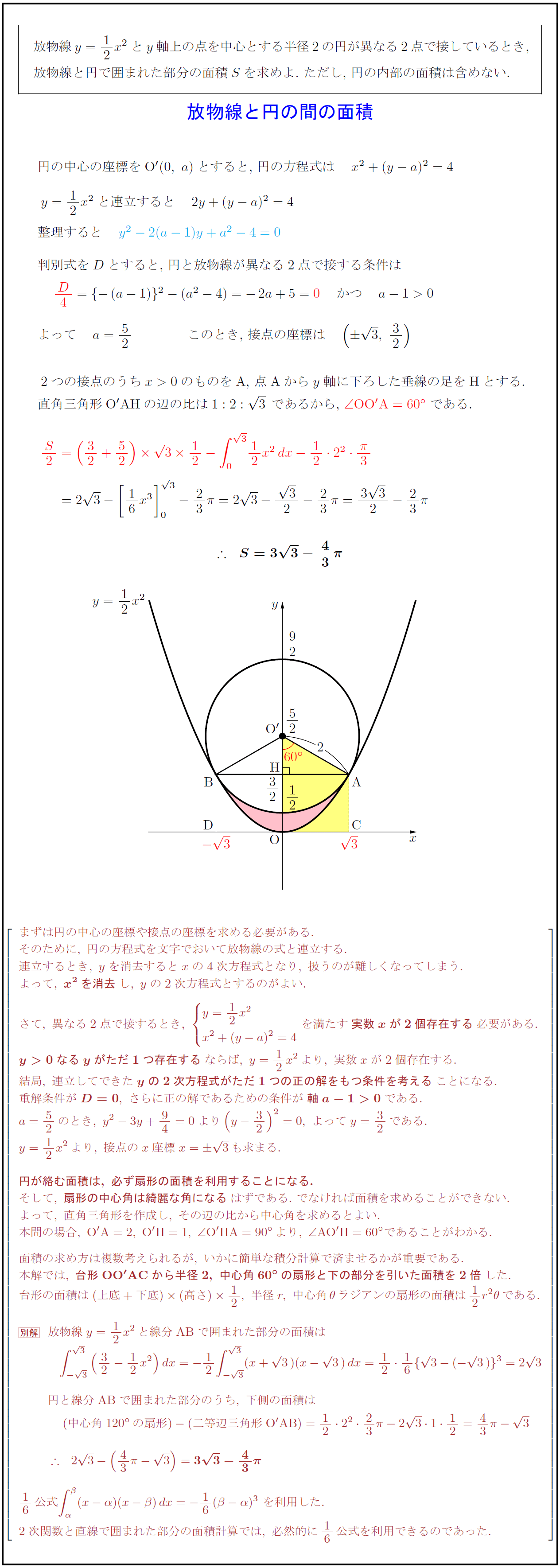



高校数学 放物線と円の間の面積 受験の月
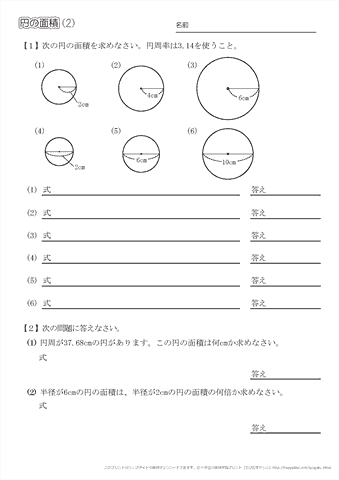



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋




微分でつなげる円や球の公式 すうがくブログ 式変形ch
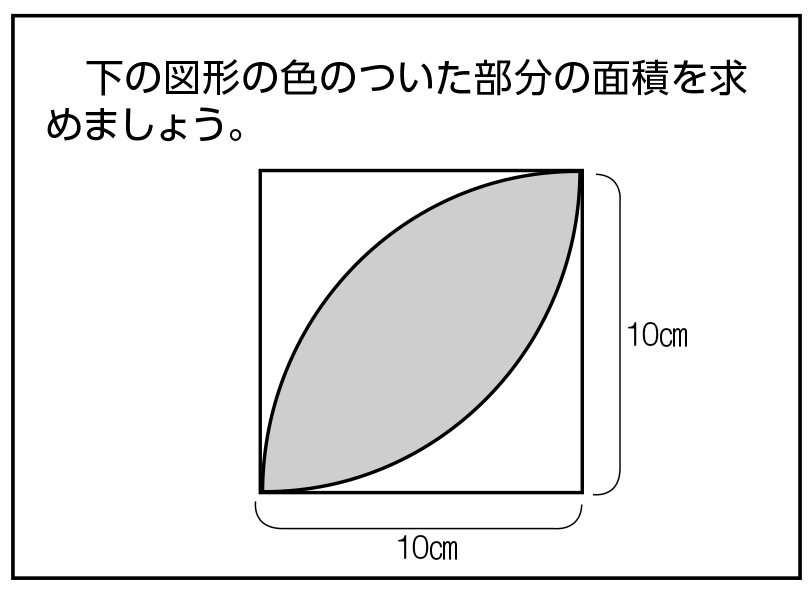



小6算数 円の面積 指導アイデア 2 みんなの教育技術




円の面積の求め方 公式と計算例




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題
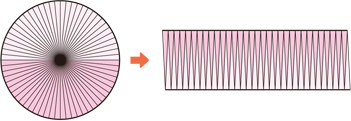



円の面積 算数用語集
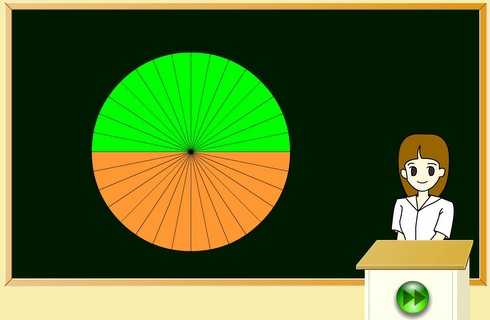



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




小6 算数 小6 2 円の面積 応用編 Youtube
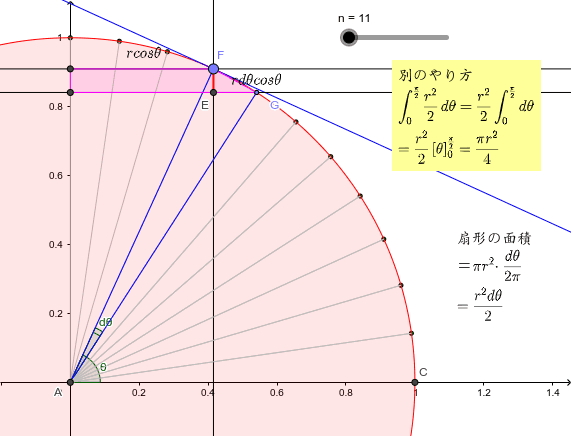



円の面積2 Geogebra



3



円の面積 半径




円の面積の求め方 公式と計算例
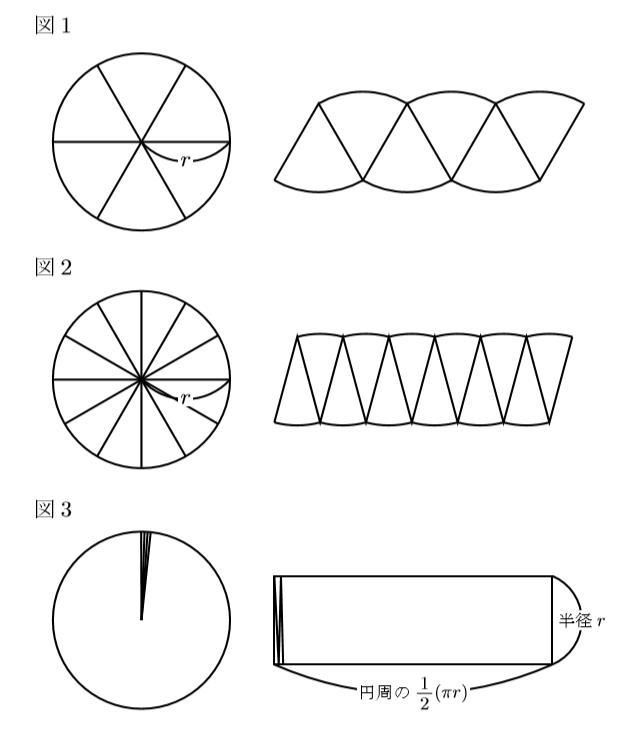



中学数学 円の面積の公式が成り立つ理由 数樂管理人のブログ




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円の面積 その2 家庭学習レシピ




小6 算数 小6 旧 円の面積 Youtube
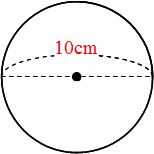



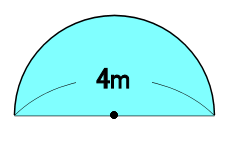
世界一やさしい 円の面積を求める問題の解き方 働きアリ
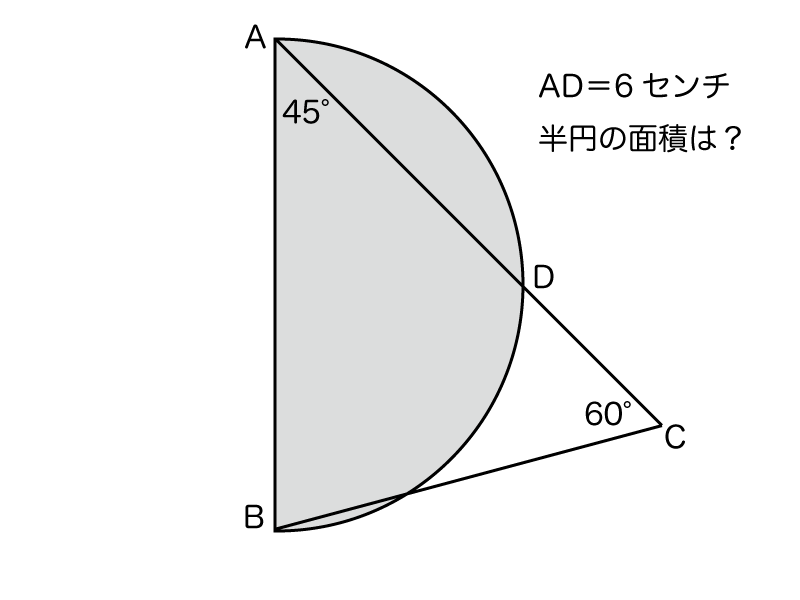



面積公式を組み合わせて解く半円の面積計算 受験算数入門



円の面積と公式 面積計算機
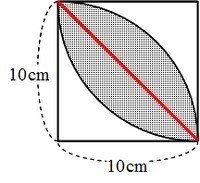



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note
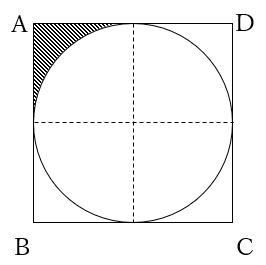



半径の分からない円の面積 中学受験プロ講師ブログ
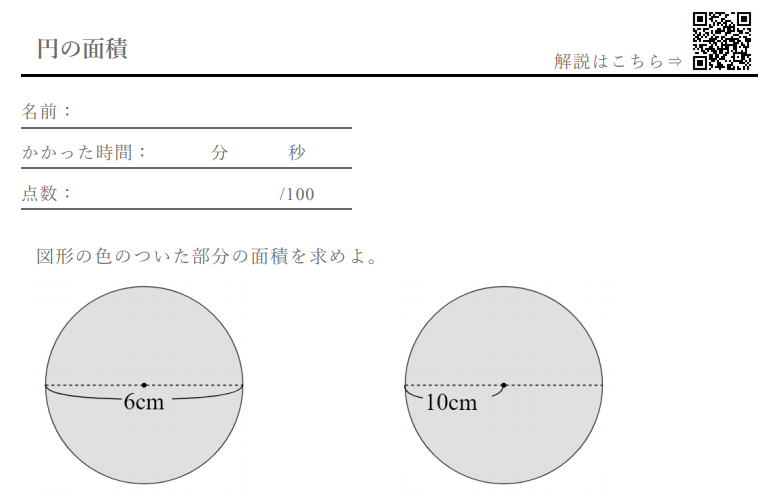



円 の面積 計算ドリル 問題集 数学fun




円の面積 練習応用 Youtube
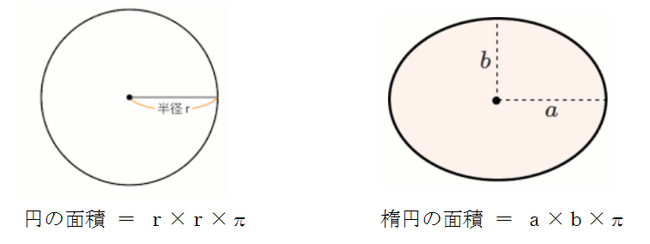



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント
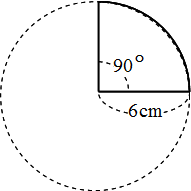



世界一やさしい 円の面積を求める問題の解き方 働きアリ
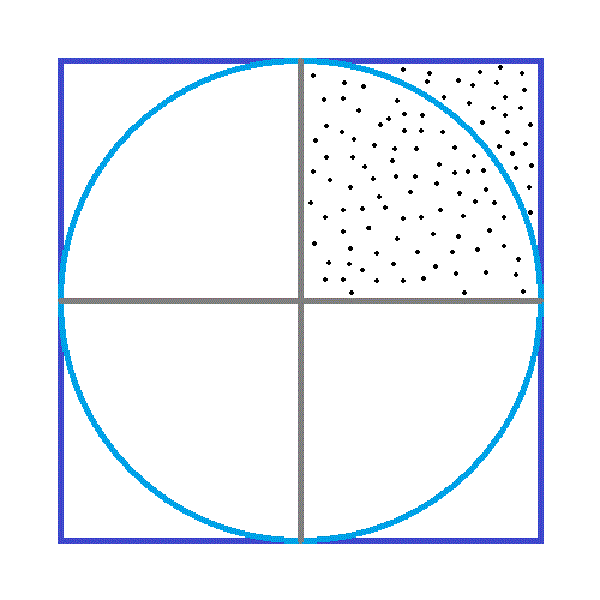



モンテカルロ法による円の面積計算




円周の求め方と円の面積について アタリマエ




円 扇形 の面積 周や弧の長さの公式 数学fun



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora



円の面積の公式 この問題をやれば円の面積は余裕だぜ 三重の個人契約家庭教師
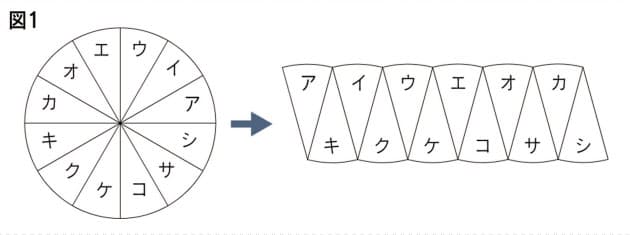



子供に説明できる 円の面積の公式 の証明 Nikkei Style




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



6年算数 円の面積 2 わかる教え方



1




円の面積 円周の求め方 苦手な数学を簡単に
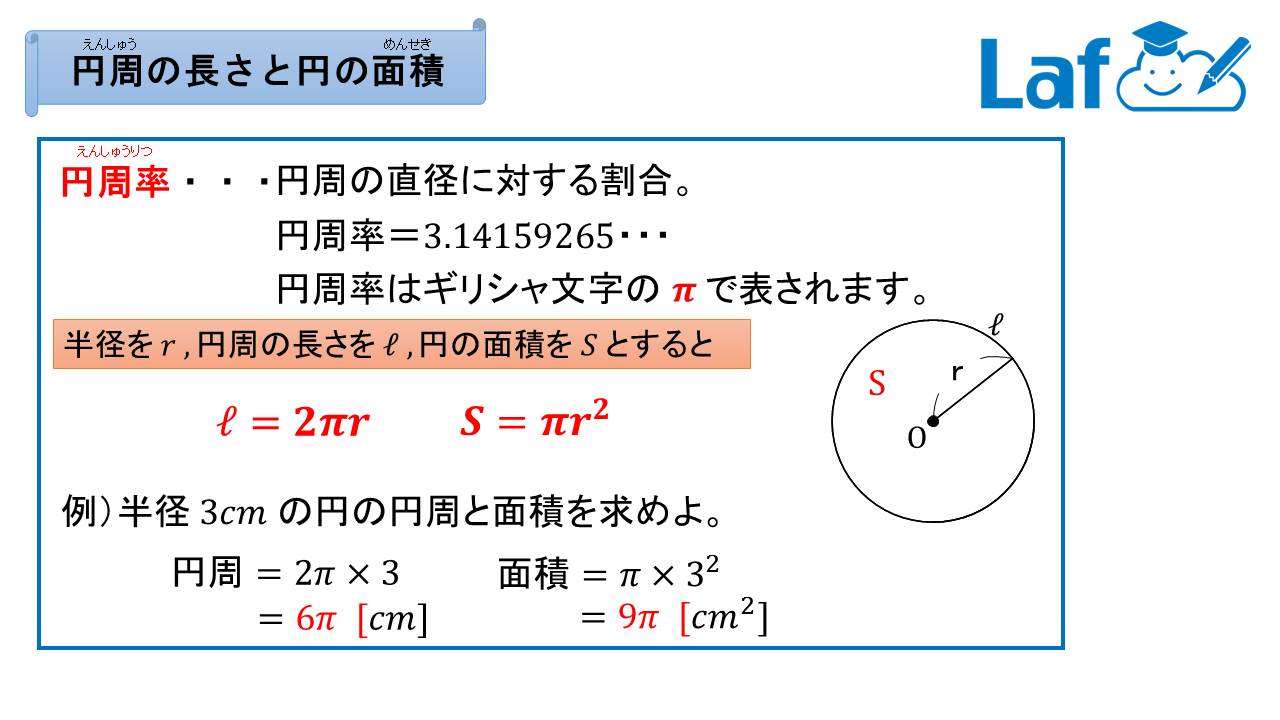



押川 隼也 高校 大学受験対策 中1数学 円周率p 円の面積 円周の長さ 1年生は事前に知っておいて損はなし 2年生は今のうちに軽く目を通して思い出しましょう 3年生は知っていたらrt 3年生は覚えてなかったらふぁぼって暗記




6年生算数ドリル 円




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
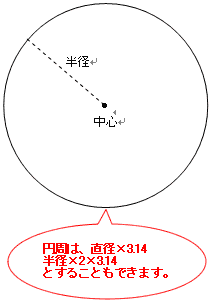



面積の考え方 算数の教え上手 学びの場 Com
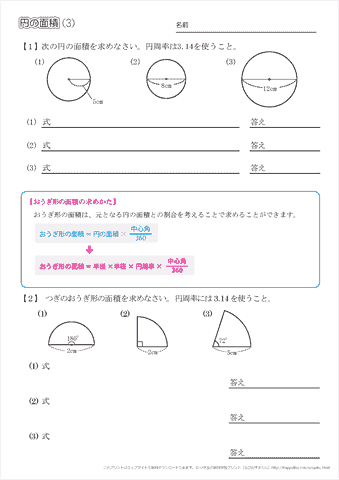



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ



円の面積 置換法の意味 Geogebra




アルゴリズム 2つの円の重なった面積 Teratail




円の面積




円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 中学数学




円の面積の求め方 公式と計算例




円の面積 算数用語集



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル



円積率 雑学のソムリエ



子供に説明できる 円の面積の公式 の証明 Nikkei Style




勉強しよう数学 円の面積を積分で求める



円の面積 簡単に計算できる電卓サイト



こどもプリント 円の面積 無料プリント



円 面積の計算 計算サイト



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



積分 円の面積の再考 大人が学び直す数学




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
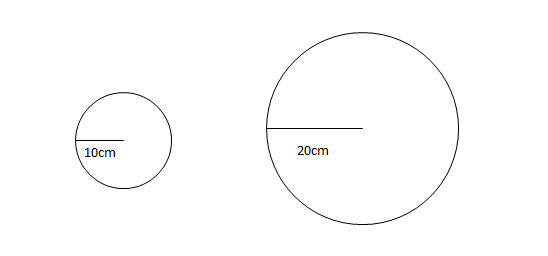



小学算数 円の半径と面積と円周の関係を理解しよう 偏差値40プログラマー



問題93おうぎ形の面積




半円や4分の1の円 四分円 の面積を計算する方法 白丸くん



1
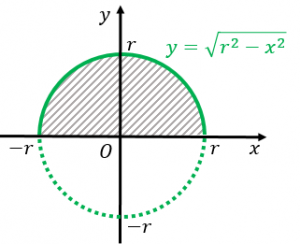



円の面積を積分で計算する2通りの方法 具体例で学ぶ数学



今週は灘より1問です 06 05 15 学習塾ロジム 今週の1問
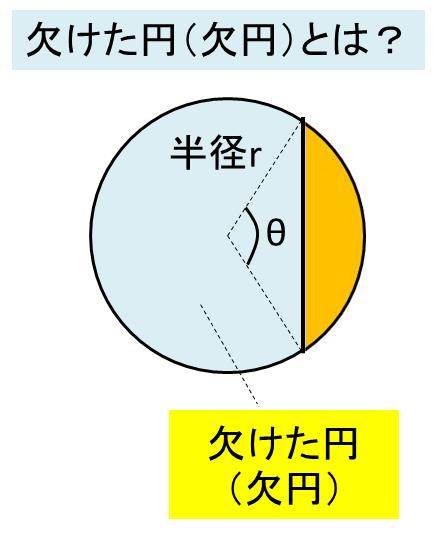



欠けた円 欠円 や弓形の面積の計算方法




6年算数 円の面積 1 アニメでわかる教え方
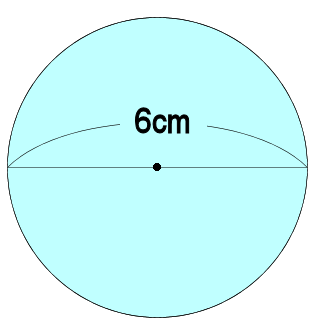



円の面積 直径



6年算数 円の面積 2 わかる教え方
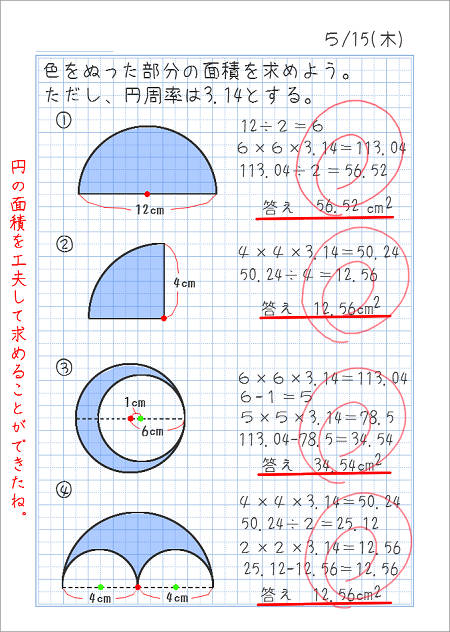



円の面積 その1 家庭学習レシピ
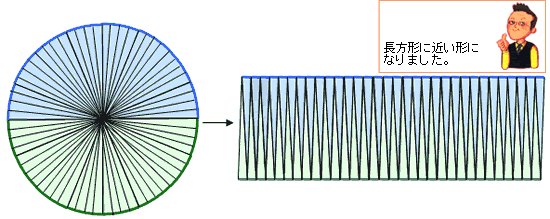



面積の考え方 算数の教え上手 学びの場 Com
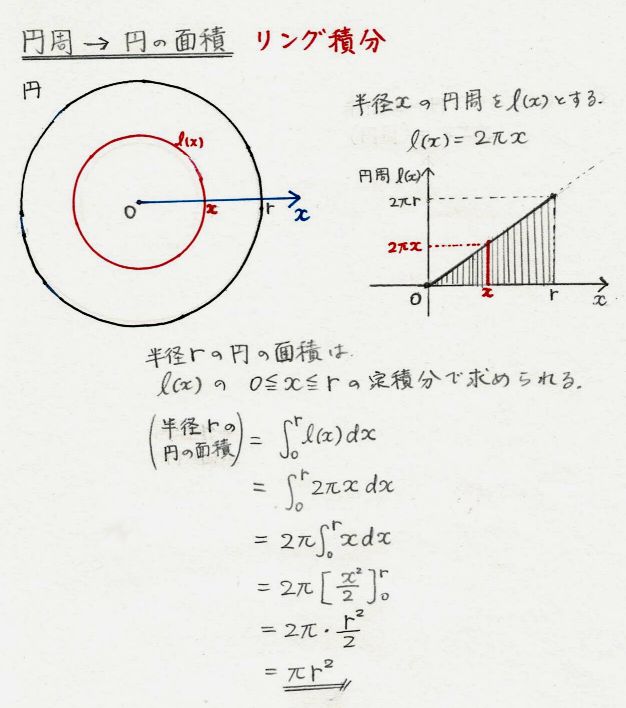



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
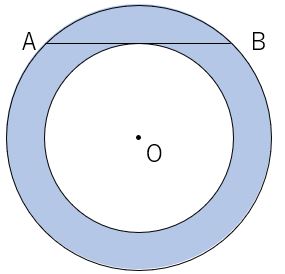



面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ
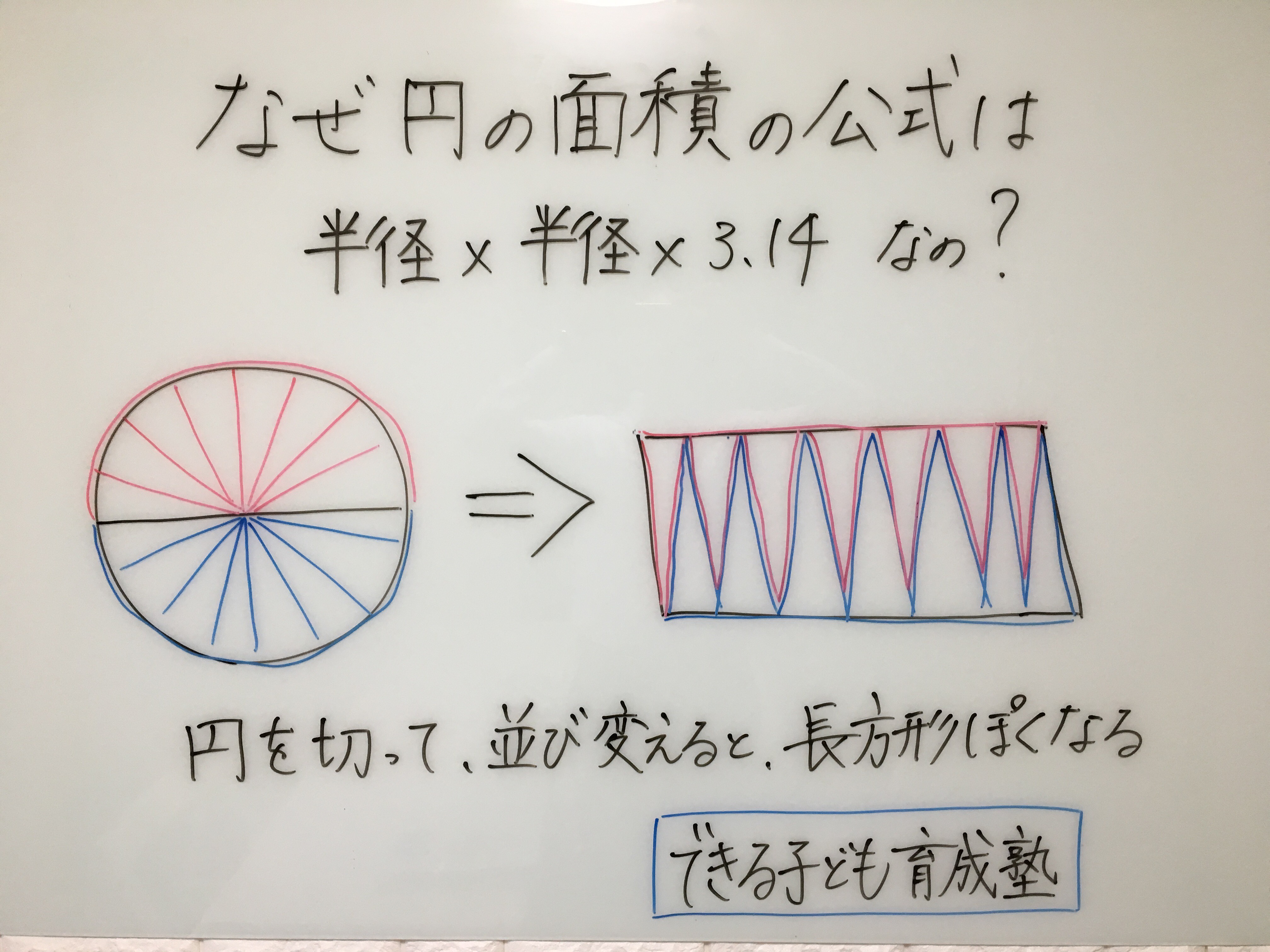



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



0 件のコメント:
コメントを投稿