正の整数の約数の総和を表す公式を2つ紹介します。 1つ目は入試でも頻出の必須公式です。 2つ目はコサインが出てくる観賞用の公式です。玄人向け。 なお,約数の個数に関しては約数の個数の公式と平方数の性質を参照して下さい。めざす姿は 倍数や約数の求め方を説明できるようになりましょう。 (1)倍数について答えましょう。 ①3の倍数を小さい方から7つかきましょう。 ②かいた3の倍数を偶数と奇数に分けましょう。 ③3と7の公倍数を小さい方から2つかきましょう。 最小公倍数は、最大公約数とそれぞれのオリジナル因数を取り出して掛け合わせた値になります。 なので、素因数分解をした式を書き並べ、 それぞれの因数の個数が大きいものを取り出していけばOKです。 答え (1)最大公約数 , 最小公倍数 次に(2)3

最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ
約数と倍数 公式
約数と倍数 公式- 基本編(約数、公倍数公約数)の実践編です。 (1)約数の数が3個あり、約数を全て足すと463になる自然数を求めなさい。 (2)504の約数の中で、4の倍数である約数の総和を求めなさい。 (3)150の約数の逆数の和と2約数と倍数 何回9で割り切れるか調べる! (立教女学院中学 11年) 最大公約数と和の関係を解く! (開成中学 14年) にあてはまるもっとも小さな数は? (攻玉社中学 14年) どの数字を打ちまちがえた? (15年 東京学芸大学附属世田谷中学)




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support
公倍数と公約数の違いを下記に示します。 公倍数 ⇒ 2つ以上の整数に共通する倍数 公約数 ⇒ 2つ以上の整数に共通する約数 倍数、約数の詳細は下記が参考になります。 倍数とは?1分でわかる意味、計算、3と8の倍数、公倍数との違い 約数とは?解 約数の総和を求めるには、素因数分解したときにでてくる同じ素因数のパーツの総和を掛けたものになります。 約数の総和を求める公式 のとき の正の約数の総和は, なぜこのようなやり方で約数の総和を求めることができるのでしょうか。 の約数と倍数についての例題をいくつか紹介していきます。 例題 (倍数の利用) a、bが整数だとすると、ab、bが3の倍数ならば、aは3の倍数であることを証明せよ。 解答 ab、bが3の倍数であるので、整数k、lを使って、 \(ab=3k,b=3l\) と表せる。よって、
「数の入門と算数 」シリーズは今回で 完結 です。 最終回 のテーマは「 素因数分解 , 約数の個数と総和 , 公約数と公倍数 」です。 前々回( 約数と倍数 素数と素因数分解 ) 、 前回( 指数のしくみ 約分と素因数分解 ) 、と続いてきた「 素因数分解 3 部作 」の 完結編 になります。 整数の性質|約数と倍数について 今回から「整数の性質」の単元になります。 まず学習するのは、約数と倍数についてです。 小中学校で学習した内容の続きになるので、忘れていないか確認しながら取り組みましょう。 1 約数と倍数、倍数の判定法 約数・倍数とあまり③ 今月は苦手な子の多い「約数・倍数とあまり」を、 第1回 問題文を式にする 第2回 5パターンの区別をつける/ 公式化する 第3回 公式を利用する/ 混合タイプをマスターする の、全3回にわけて一緒に勉強していきましょう。 動画
あなたは最小公倍数とは何かわかりますか? 答えに困ってしまった人、この記事で確認していきましょう。 答えられた人も、もしかしたら最小公倍数の性質を全てはわかっていないかもしれません。 この記事では、最小公倍数の意味や求め方といった基礎の解説から始まり、から、大学 約数・倍数とあまり① 今月は苦手な子の多い「約数・倍数とあまり」を、 第1回 問題文を式にする 第2回 5パターンの区別をつける/ 公式化する 第3回 公式を利用する/ 混合タイプをマスターする の、全3回にわけて一緒に勉強していきましょう。 動画 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 の倍数の判定法をまとめました!!
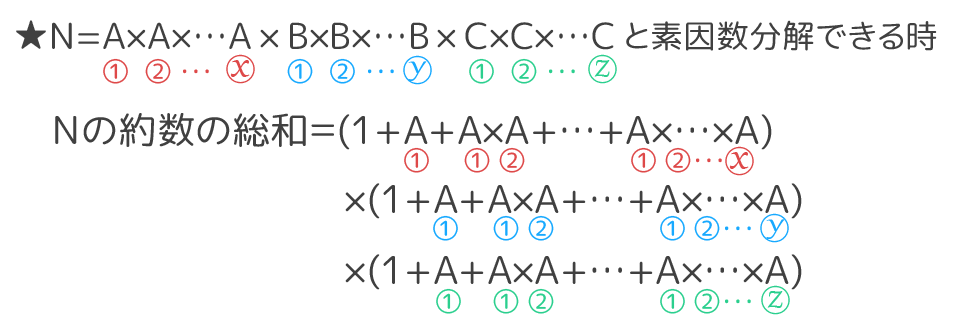



約数の総和の求め方 そうちゃ式 受験算数 新1号館 数論 特殊算




高2 因数定理と整式の倍数 約数 高校生 数学のノート Clear
2つの整数 a, b について、 a = bk a = b k を満たす整数 k k があるとき、 b は a の 約数 (divisor) であるといい、 a は b の 倍数 (multiple) である、といいます。数の性質といってまず頭に浮かぶのは「約数と倍数」でしょう。 「約数と倍数」は、5年生で基本を習った後、 再び6年生の2月に学習することが多いようです。 ということで 「6年生になると、5年生のときと何が変わるか」 をみておきましょう。正の約数の個数と総和を求める公式の解説~高校数学 (数A)場合の数 今回は、 正の約数の個数とその総和 、についてオリジナル問題で解説します。 この例題は、教科書レベルや白チャートや黄色チャートの基本レベルなので、定期テスト対策などで困って



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ




約数の個数の求め方を超わかりやすく説明してみた 理系ラボ
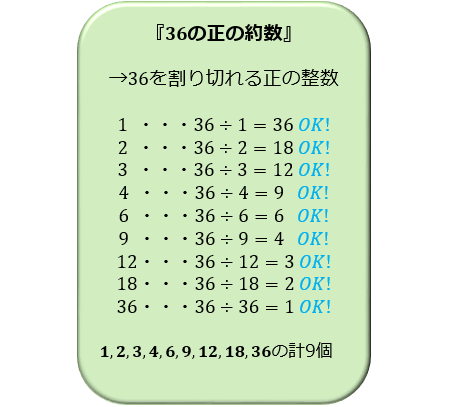
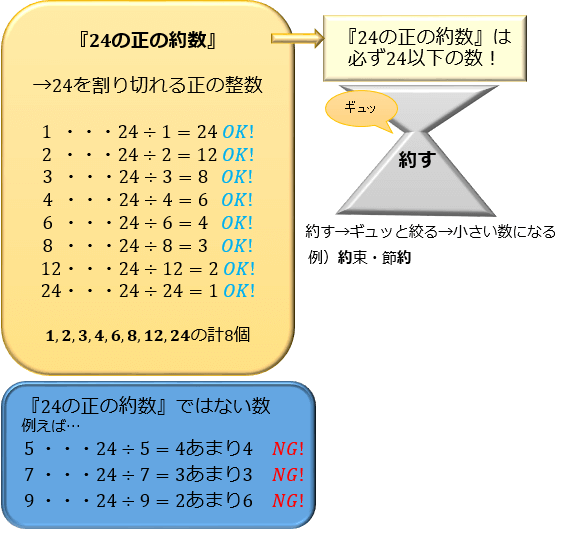
競技プログラミングで倍数・約数変換を使う場面は主に以下の二つが考えられる。 (1) f (i) (1 ≤ i ≤ n) f ( i) ( 1 ≤ i ≤ n) が与えられた時に g(j) (1 ≤ j ≤ n) g ( j) ( 1 ≤ j ≤ n) を求める (2) f (i) (i ∣ n f ( i) ( i ∣ n または n ∣ i) n ∣ i) が与えられた時に g(n) g ( n 約数の総和を求める公式! 約数の総和を求める公式です。 \ (a^x\cdot b^y\cdot c^z\)と素因数分解できたときその数の約数の総和は $$ (a^0a^1\cdots a^x) (b^0b^1\cdots b^y) (c^0c^1\cdots c^z)$$ となります。 例題の②,③では式を上の公式で立てずに全ての約数を 最大公約数まとめ ①最大公約数とは、 公約数の中で一番大きな数 のこと。 「2つ以上の正の整数に共通する約数の中で一番大きい数」を指す ②約数は、必ず「元の数と同じか、それよりも小さな数」になる。 24 の約数は必ず 24 以下であり、 36 の約数は



1




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座
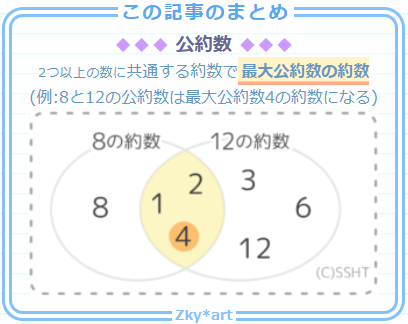
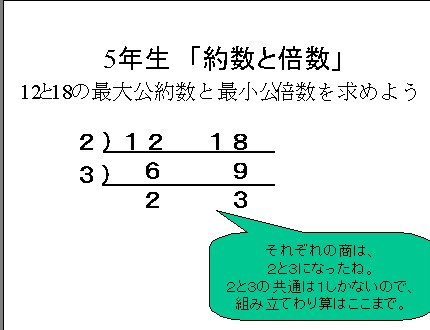
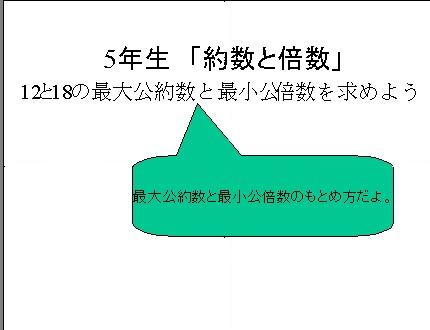
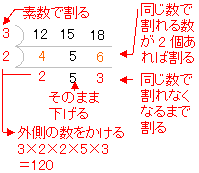
約数 約数ある整数を割り切れることができる整数。 18の約数1、2、3、6、9、18 素数約数が1とその数しかない整数 2、3、5、7、11、13、17、最大公約数,最小公倍数とは 2つ以上の正の整数に共通な約数(公約数)のうち最大のものを最大公約数といいます. 例 12 と 18 の公約数は, 1,2,3,6 で, 6 が最大公約数 2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを最小公倍数といいます.約数と倍数 - カテゴリー 全 4 件の記事が見つかりました。 19年7月30日 最大公約数と最小公倍数の計算方法を解説します。まず、基本的な計算方法として、素因数分解を用いた計算方法を復習した




小5 算数 小5 倍数 約数の文章題 Youtube



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 012 Pdf
今回の問題は「 約数と倍数 」です。 問題 次の問いに答えよ。 の正の約数をすべて答えよ。 の約数をすべて答えよ。 の倍数を書き並べよ。 の正の倍数を小さい方から5つ答えよ。 次のページ「解法のPointと問題解説」 次へ 約数と倍数・倍数の判定方法の説明のおわりに いかがでしたか? 倍数判定方法を忘れてしまった場合には、実際に割ってみて割り切れるかどうかを確認すれば問題ありません。 その数の倍数であるかどうかはその数を約数に持つかどうかですので道具を用いて,素数の個数を表す公式に迫りたい. 1 約数,倍数,素数 自然数a,bについて,a = bcとなる自然数cがあるとき,bはaの約数,aはbの 倍数という.例えば,15 = 3×5だから,3は15の約数,15は3の倍数である.



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ
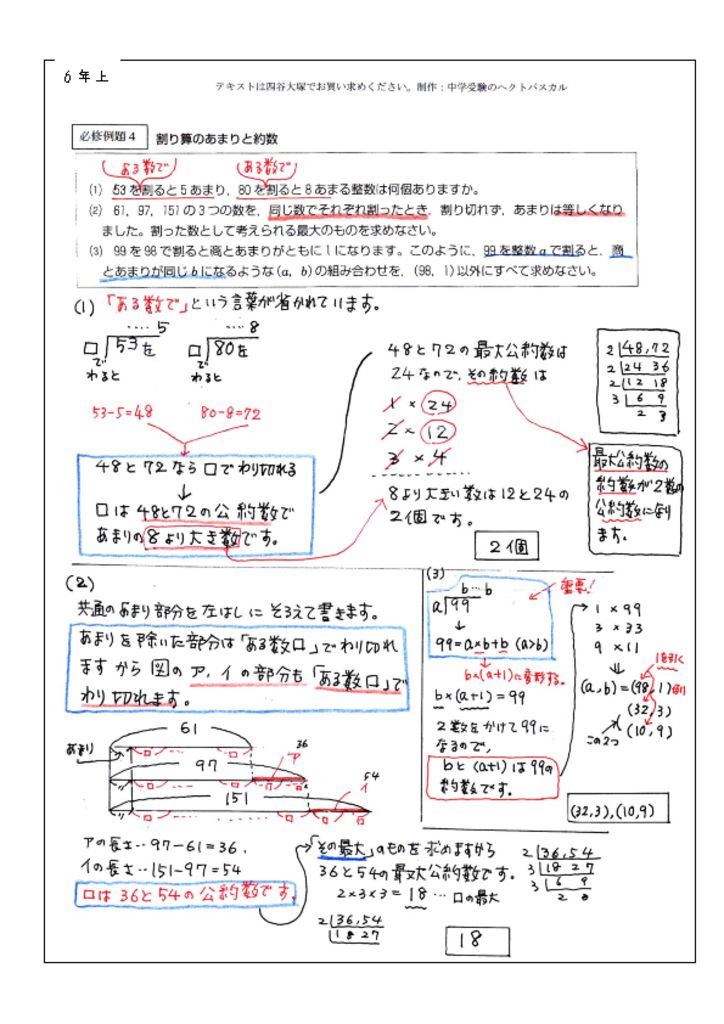



割り算のあまりと約数 数の問題 中学受験の算数 理科ヘクトパスカル




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




第回 数の性質 約数と倍数 分数 6年生 日能研の歩き方




競プロ 素因数分解と約数と倍数 なかけんの数学ノート




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




倍数と約数 小5 公倍数 公約数 手探るは最強の解き方 算数の教え方教えますmother S Math Happy Study Support



5年算数整数 教え方のポイント




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ



Studydoctor約数 倍数とは その求め方 Studydoctor




倍数 約数 算数用語集




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ




公約数 公倍数の求め方 Z Square Z会




倍数と約数の教え方 2 公倍数と公約数は小さな数のかけ算の形にしてみる ママのための受験算数の教え方プチ講座 中学受験ナビ
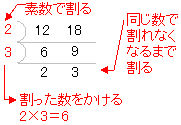



約数 倍数
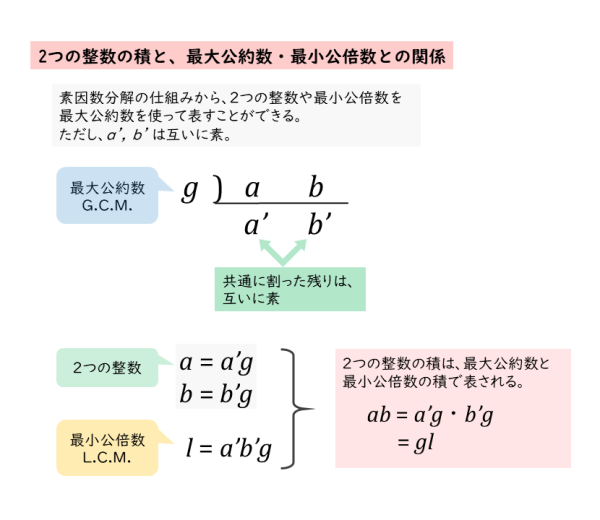



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん
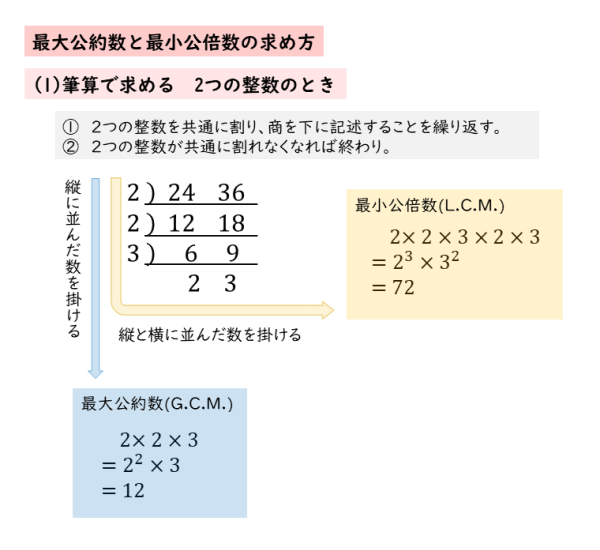



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




競プロ 素因数分解と約数と倍数 なかけんの数学ノート



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html




クリアー数学a 数a P141 21 約数と倍数



約数と倍数 中学受験ー算数解き方ポータル



倍数 公倍数 最小公倍数 通分 分数のたし算ひき算の授業 教材 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



問題文は 24の倍数で正の約数が15個であるような自然数を求めよ という Yahoo 知恵袋
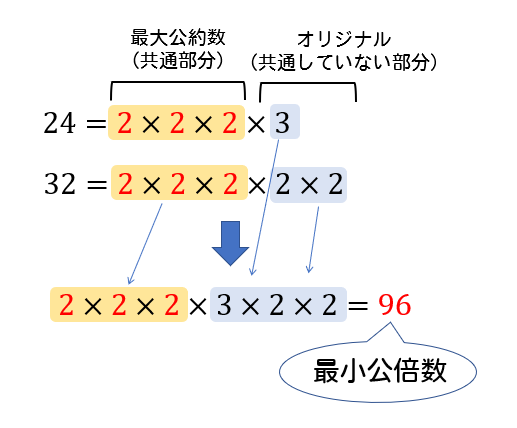



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ




約数と倍数 素数と素因数分解




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学
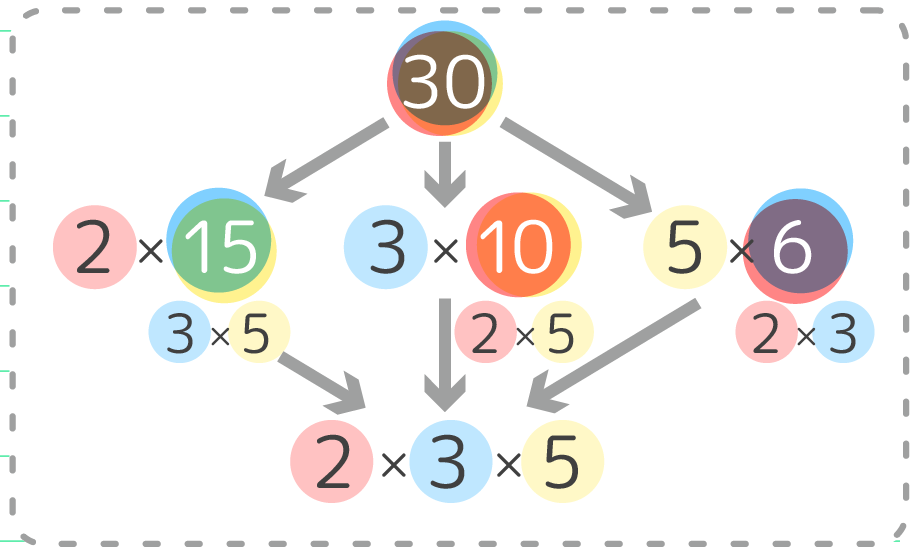



中学受験 素数 約数と すだれ算 での素因数分解のやり方 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算




数a 28の倍数で正の約数の個数が15こである自然数nを全て求めよ とい 数学 教えて Goo



倍数約数 公倍数公約数 そうちゃ式 分かりやすい図解算数 別館




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
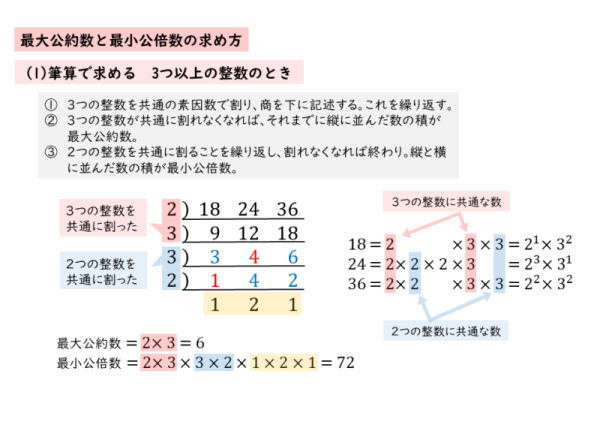



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ




数学a 約数の個数と総和を求める公式は 問題を使って解説 数スタ




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



3




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生
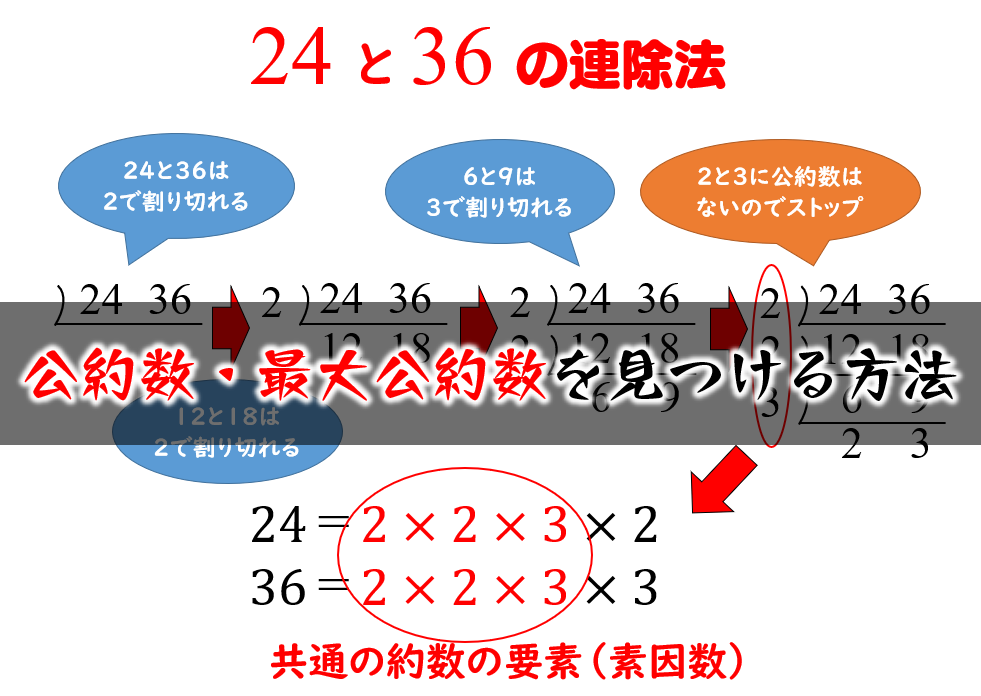



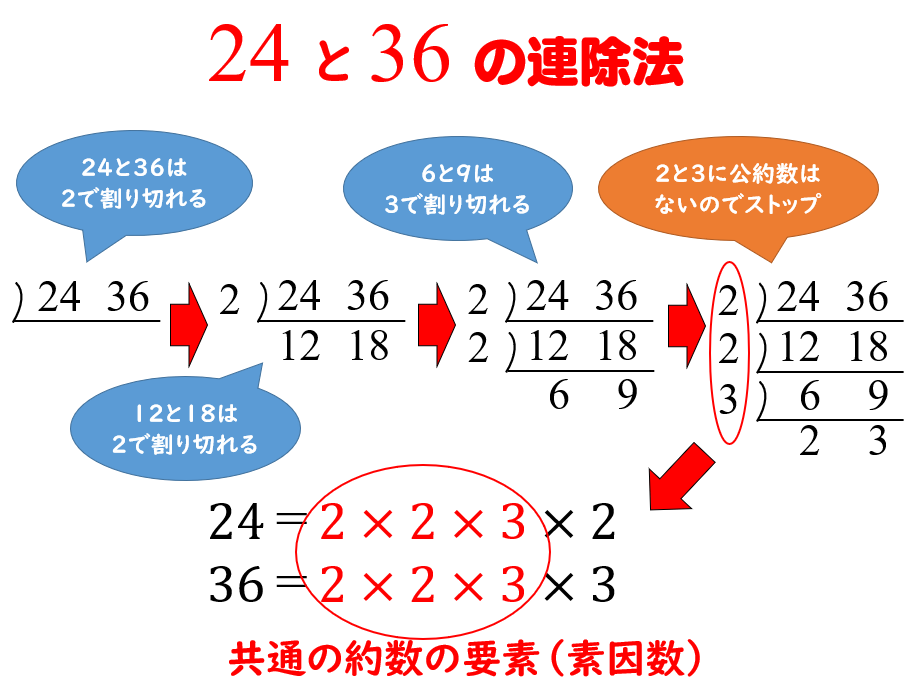
公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
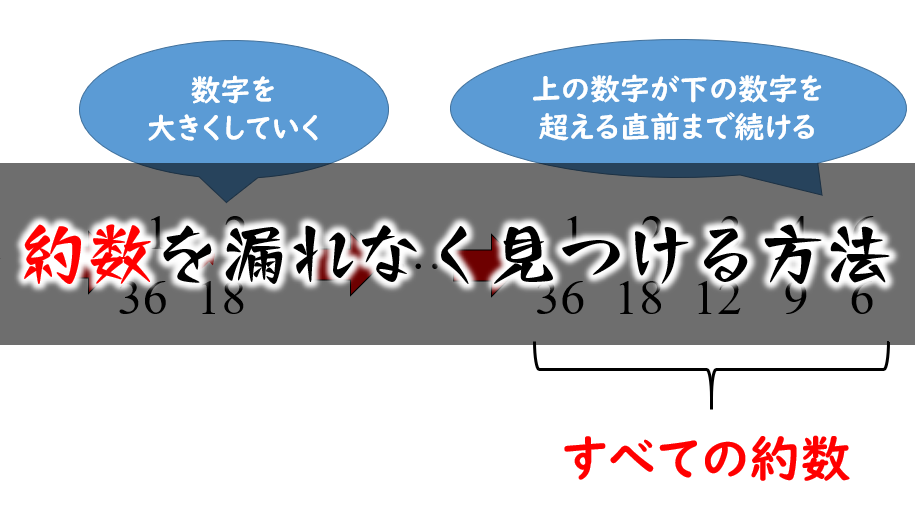



約数を漏れなく簡単に見つける方法 小学生でも素因数分解ができると便利 数学fun




教科書レベルの問題一覧と解答 数学a 整数の性質 教科書より詳しい高校数学




最小公倍数と最大公約数の式 倍数 約数シリーズ Youtube




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




小5 算数 小5 約数 公約数 最大公約数 Youtube



算数4年から6年




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生
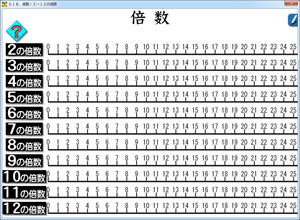



5年の算数ソフト 倍数と約数 さくら社



6 約数の数と合計の問題 京極一樹の数学塾




小学生 約数のノート一覧 Clear




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support
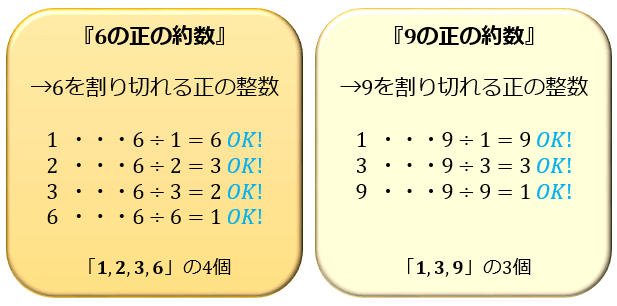



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ



算数4年から6年




高校数学 数a 勉強動画 約数と倍数 の問題 19ch




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



約数 倍数




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質



ドリルズ 小学5年生 算数 の無料学習プリント算数 倍数と約数




100までの数 倍数一覧表 約数一覧表 Yattoke 小 中学生の学習サイト




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数 最大公約数を求める 練習問題 Youtube




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




数の性質 公務員試験の基礎と競馬のデータ




高1 数学a 2章 1節 約数と倍数 3節 整数の性質の活用 高校生 数学のノート Clear




最大公約数と最小公倍数の積の性質の2通りの証明 高校数学の美しい物語




小5 算数 小5 20 倍数 約数の文章題 Youtube



3



48s96ub7b0z5f Net Seisuu Yakusuu




高校数学 数a 5 場合の数 正の約数編 Youtube




高校数学a 約数と倍数 整数問題の極意 受験の月



3




倍数と約数再び 正しい理解のために 身勝手な主張




数の性質 公務員試験の基礎と競馬のデータ




倍数表 約数表 石原清貴の算数教育ブログ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




数aの整数 約数と倍数の分野です 赤チャートです 教えてくださいっm M Clear




倍数 最小公倍数と約数 最大公約数を教えてみた 妹z会中学受験コース4年




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




5400の正の約数の中で 30の倍数の個数を求めなさい Clear




Q 24の倍数で せいの約数の個数が21個である自然数nを求めよ Clear




約数と倍数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




倍数 約数 算数用語集




倍数約数 公倍数公約数 そうちゃ式 分かりやすい図解算数 別館
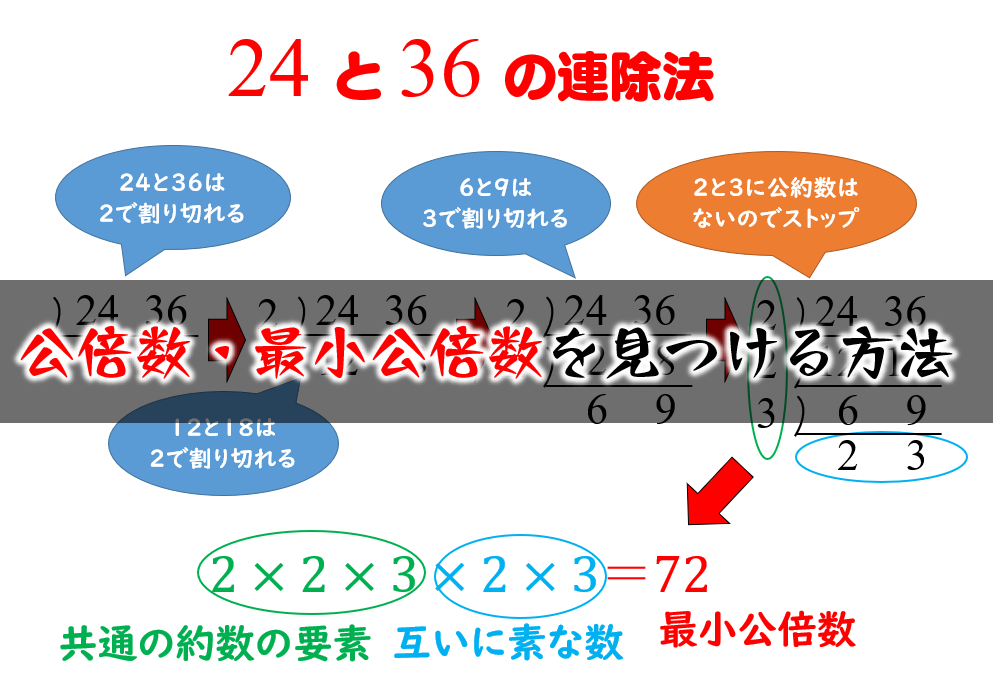



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
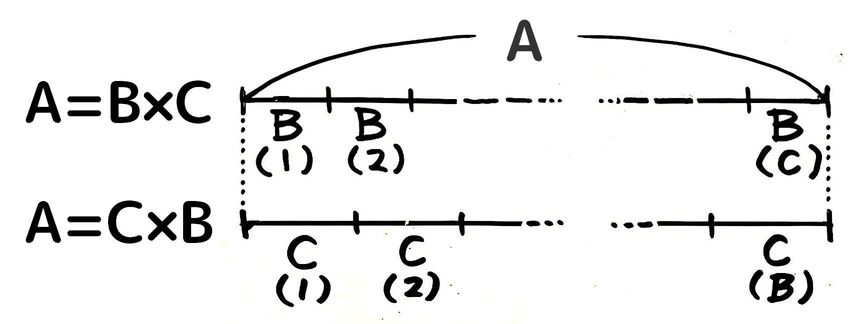



小学5年生 約数 公約数の意味と求め方は 書き出し式 プリントあり そうちゃ式 分かりやすい図解算数 別館




倍数もしくは約数である関係についての推移律 タロウ岩井の数学と英語 Note




小5 算数 小5 19 約数と公約数 Youtube




倍数と約数再び 正しい理解のために 身勝手な主張




新企画 合判模試の準備をしよう 基礎編 倍数 約数 受験情報ブログ 首都圏模試センター




約数の個数と約数の総和の求め方とは 公式は素因数分解で導きます 遊ぶ数学




中学受験 算数確認チェック13 数の性質 約数 倍数 グランパは元塾長



倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




高校数学 数a 65 約数と倍数 Youtube
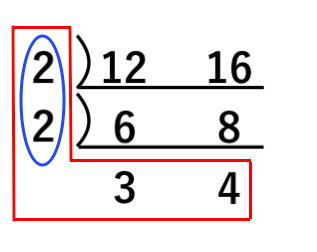



最大公約数と最小公倍数のひみつ 苦手な数学を簡単に



0 件のコメント:
コメントを投稿